



Next: 4.12 Sulfur Chemistry
Up: 4. Model Physics
Previous: 4.10 Surface Exchange Formulations
Contents
Subsections
4.11 Vertical Diffusion and Boundary Layer Processes
The vertical diffusion parameterization in CAM 3.0 provides the
interface to the turbulence parameterization, computes the molecular
diffusivities (if necessary) and finally computes the tendencies of
the input variables. The diffusion equations are actually solved
implicitly, so the tendencies are computed from the difference between
the final and initial profiles.
In the near future, the gravity wave parameterization will also be
called from within the vertical diffusion. This will allow the
turbulent and, especially, the molecular diffusivity to be passed to
the gravity wave parameterization to damp vertically propagating
waves. The gravity wave parameterization may return additional
diffusivities and tendencies to be applied before the actual diffusion
is applied.
As in CCM2 and CCM3, the turbulence parameterization in CAM 3.0 includes
computation of diffusivities for the free atmosphere, based on the
gradient Richardson number, and an explicit, non-local Atmospheric
Boundary Layer (ABL) parameterization. The ABL parameterization
includes a determination of the boundary layer depth. In practice, the
free atmosphere diffusivities are calculated first at all levels. The
ABL scheme then determines the ABL depth and diffusivities and
replaces the free atmosphere values for all levels within the ABL,
returning both the updated diffusivities and the non-local transport
terms. The implementation of the ABL parameterization in CCM2 is
discussed in [74], while the formalism only is discussed
here. Following the ABL scheme, molecular diffusivities are computed
if the model top extends above  90 km (0.1 Pa).
90 km (0.1 Pa).
As described in Boville and Bretherton [25], a general vertical diffusion
parameterization can be written in terms of the divergence of
diffusive fluxes:
where
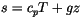 is the dry static energy,
is the dry static energy, 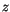 is the
geopotential height above the local surface (does not include the
surface elevation) and
is the
geopotential height above the local surface (does not include the
surface elevation) and 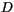 is the heating rate due to the dissipation
of resolved kinetic energy in the diffusion process. The diffusive
fluxes are defined as:
is the heating rate due to the dissipation
of resolved kinetic energy in the diffusion process. The diffusive
fluxes are defined as:
The viscosity 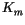 and diffusivities
and diffusivities 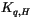 are the sums of:
turbulent components
are the sums of:
turbulent components
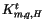 , which dominate below the
mesopause; and molecular components
, which dominate below the
mesopause; and molecular components 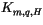 , which dominate above
120 km. The turbulent diffusivities are the sum of two components,
free atmosphere and boundary layer diffusivities, defined below. In
the future, these terms also may include effective diffusivities from
the gravity wave parameterization. The non-local transport terms
, which dominate above
120 km. The turbulent diffusivities are the sum of two components,
free atmosphere and boundary layer diffusivities, defined below. In
the future, these terms also may include effective diffusivities from
the gravity wave parameterization. The non-local transport terms
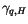 are given by the ABL parameterization. Note that
are given by the ABL parameterization. Note that
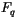 , as defined in (4.451) and implemented in CAM 3.0, does
not include the term which causes diffusive separation of constituents
of differing molecular weights. The molecular diffusion in CAM 3.0 is
currently incomplete and should be used with caution. The molecular
viscosity and diffusivities are all currently defined as
, as defined in (4.451) and implemented in CAM 3.0, does
not include the term which causes diffusive separation of constituents
of differing molecular weights. The molecular diffusion in CAM 3.0 is
currently incomplete and should be used with caution. The molecular
viscosity and diffusivities are all currently defined as
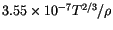 . A more complete form, allowing separation of
constituents, will be implemented later.
. A more complete form, allowing separation of
constituents, will be implemented later.
The kinetic energy dissipation term 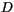 in (4.449) is
determined by forming the equation for total energy from
(4.448-4.449):
in (4.449) is
determined by forming the equation for total energy from
(4.448-4.449):
The diffusive kinetic energy flux in (4.454) is
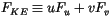 |
(4.455) |
and the kinetic energy dissipation is
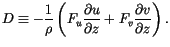 |
(4.456) |
To show that 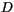 is positive definite, we use (4.450) to
expand for
is positive definite, we use (4.450) to
expand for 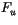 and
and 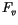 :
:
![$\displaystyle D = (K_m^t + K_m^m) \left[ \left(\frac{\partial u}{\partial z}\right)^2 +\left(\frac{\partial v}{\partial z}\right)^2 \right] \ge 0.$](img2562.gif) |
(4.457) |
We show that energy is conserved in the column by integrating
(4.454) in the vertical, from the surface (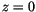 ), to the
top of the model (
), to the
top of the model (
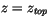 ):
):
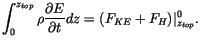 |
(4.458) |
Therefore, the vertically integrated energy will only change because
of the boundary fluxes of energy, of which only the surface heat flux,
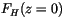 , is usually nonzero. It is typically assumed that the
surface wind vanishes, even over oceans and sea ice, giving
, is usually nonzero. It is typically assumed that the
surface wind vanishes, even over oceans and sea ice, giving
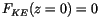 . Then, the surface stress
. Then, the surface stress
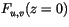 does not
change the total energy in the column, but does result in kinetic
energy dissipation and heating near the surface (see below) For
coupled models, nonzero surface velocities can be accommodated by
including
does not
change the total energy in the column, but does result in kinetic
energy dissipation and heating near the surface (see below) For
coupled models, nonzero surface velocities can be accommodated by
including 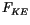 on both sides of the surface interface.
on both sides of the surface interface.
The free atmospheric turbulent diffusivities are typically taken as
functions of length scales 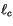 and local vertical gradients of
wind and virtual potential temperature, e.g.
and local vertical gradients of
wind and virtual potential temperature, e.g.
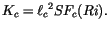 |
(4.459) |
Here 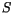 is the local shear, defined by
is the local shear, defined by
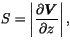 |
(4.460) |
and the mixing length 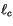 is generally given by
is generally given by
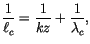 |
(4.461) |
where  is the Von Karman constant, and
is the Von Karman constant, and 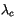 is the so-called
asymptotic length scale, taken to be 30 m above the ABL. Since the
lowest model level is always greater than 30 m in depth,
is the so-called
asymptotic length scale, taken to be 30 m above the ABL. Since the
lowest model level is always greater than 30 m in depth, 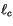 is
simply set to 30 m in CAM 3.0. Furthermore,
is
simply set to 30 m in CAM 3.0. Furthermore, 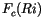 denotes a
functional dependence of
denotes a
functional dependence of 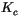 on the gradient Richardson number:
on the gradient Richardson number:
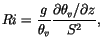 |
(4.462) |
where 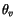 is the virtual potential temperature,
is the virtual potential temperature,
![$\displaystyle \theta_v = \theta \left[ 1 + \left( \frac{R_v}{R} -1 \right) q \right] .$](img2578.gif) |
(4.463) |
For simplicity, in the free atmosphere, we specify the same stability
functions 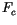 for all
for all 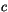 . For unstable conditions
. For unstable conditions 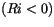 we
choose
we
choose
This means that no distinction is made between turbulent vertical
diffusion of heat, scalars and momentum outside the boundary
layer. However, separate coefficient arrays are maintained and other
parameterizations (such as gravity wave drag) may provide distinct
diffusivities. We also note the the turbulent diffusivity is the same
for all constituents, even within the ABL. However, the molecular
diffusivities differ for each constituent since they depend on it's
molecular weight.
The free atmosphere turbulent diffusivities, described above, are an
example of the local diffusion approach. In such an approach, the
turbulent flux of a quantity is proportional to the local gradient of
that quantity (e.g. (4.450)-(4.451)). In addition,
the eddy diffusivity depends on local gradients of mean wind and mean
virtual temperature (see (4.459)). These are reasonable
assumptions when the length scale of the largest turbulent eddies is
smaller than the size of the domain over which the turbulence
extends. In the Atmospheric Boundary Layer (ABL) this is typically
true for neutral and stable conditions only. For unstable and
convective conditions, however, the largest transporting eddies may
have a size similar to the boundary layer height itself, and the flux
can be counter to the local gradient [76,48].
In such conditions a local diffusion approach is no longer
appropriate, and the eddy diffusivity is better represented with
turbulent properties characteristic of the ABL. We will refer to such
an approach as non-local diffusion.
To account for ``non-local'' transport by convective turbulence in the
ABL, the local diffusion term for constituent 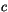 is modified as in
(4.451):
is modified as in
(4.451):
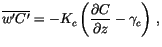 |
(4.466) |
where 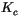 is the non-local eddy diffusivity for the quantity of
interest. The term
is the non-local eddy diffusivity for the quantity of
interest. The term 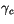 is a ``non-local'' transport term and
reflects non-local transport due to dry convection.
Eq. (4.466) applies to static energy, water vapor, and passive
scalars. No countergradient term is applied to the wind components, so
(4.450) does not contain these terms. For stable and neutral
conditions the non-local term is not relevant for any of the
quantities. The eddy diffusivity formalism is, however, modified for
all conditions.
is a ``non-local'' transport term and
reflects non-local transport due to dry convection.
Eq. (4.466) applies to static energy, water vapor, and passive
scalars. No countergradient term is applied to the wind components, so
(4.450) does not contain these terms. For stable and neutral
conditions the non-local term is not relevant for any of the
quantities. The eddy diffusivity formalism is, however, modified for
all conditions.
In the non-local diffusion scheme the eddy diffusivity is given by
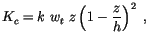 |
(4.467) |
where 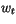 is a turbulent velocity scale and
is a turbulent velocity scale and 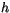 is the boundary
layer height. Equation (4.467) applies for heat, water vapor
and passive scalars. The eddy diffusivity of momentum
is the boundary
layer height. Equation (4.467) applies for heat, water vapor
and passive scalars. The eddy diffusivity of momentum 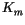 , is also
defined as (4.467) but with
, is also
defined as (4.467) but with 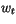 replaced by another velocity
scale
replaced by another velocity
scale 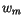 . With proper formulation of
. With proper formulation of 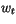 (or
(or 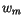 ) and
) and 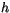 , it
can be shown that equation (4.467) behaves well from very
stable to very unstable conditions in horizontally homogeneous and
quasi-stationary conditions. For unstable conditions
, it
can be shown that equation (4.467) behaves well from very
stable to very unstable conditions in horizontally homogeneous and
quasi-stationary conditions. For unstable conditions 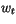 and
and 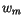 are proportional to the so-called convective velocity scale
are proportional to the so-called convective velocity scale 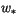 ,
while for neutral and stable conditions
,
while for neutral and stable conditions 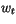 and
and 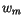 are
proportional to the friction velocity
are
proportional to the friction velocity 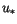 .
.
The major advantage of the present approach over the local eddy
diffusivity approach is that large eddy transport in the ABL is
accounted for and entrainment effects are treated implicitly. Above
the ABL,
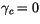 so (4.466) reduces to a local form with
so (4.466) reduces to a local form with
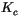 given by (4.459). Near the top of the ABL we use the
maximum of the values by (4.459) and (4.467), although
(4.467) almost always gives the larger value in practice.
given by (4.459). Near the top of the ABL we use the
maximum of the values by (4.459) and (4.467), although
(4.467) almost always gives the larger value in practice.
The non-local transport term in (4.466), 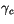 , represents
non-local influences on the mixing by turbulence
[48]. As such, this term is small in stable conditions,
and is therefore neglected under these conditions. For unstable
conditions, however, most heat and moisture transport is achieved by
turbulent eddies with sizes on the order of the depth
, represents
non-local influences on the mixing by turbulence
[48]. As such, this term is small in stable conditions,
and is therefore neglected under these conditions. For unstable
conditions, however, most heat and moisture transport is achieved by
turbulent eddies with sizes on the order of the depth 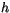 of the
ABL. In such cases, a formulation for
of the
ABL. In such cases, a formulation for 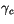 consistent with the
eddy formulation of (4.466) is given by
consistent with the
eddy formulation of (4.466) is given by
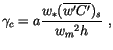 |
(4.468) |
where 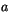 is a constant and
is a constant and
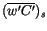 is the
surface flux (in kinematic units) of the transported scalar. The form
of (4.468) is similar to the one proposed in
Holtslag and Moeng [76]. The non-local correction vanishes under neutral
conditions, for which
is the
surface flux (in kinematic units) of the transported scalar. The form
of (4.468) is similar to the one proposed in
Holtslag and Moeng [76]. The non-local correction vanishes under neutral
conditions, for which
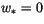 .
.
The formulations of the eddy-diffusivity and the non-local terms are
dependent on the boundary layer height 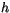 . The CCM2 configuration of
this non-local scheme made use of a traditional approach to estimating
the boundary layer depth by assuming a constant value for the bulk
Richardson number across the boundary layer depth so that
. The CCM2 configuration of
this non-local scheme made use of a traditional approach to estimating
the boundary layer depth by assuming a constant value for the bulk
Richardson number across the boundary layer depth so that 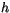 was
iteratively determined using
was
iteratively determined using
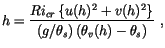 |
(4.469) |
where 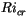 is a critical bulk Richardson number for the ABL;
is a critical bulk Richardson number for the ABL;
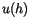 and
and 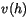 are the horizontal velocity components at
are the horizontal velocity components at 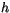 ;
;
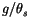 is the buoyancy parameter and
is the buoyancy parameter and
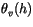 is the
virtual temperature at
is the
virtual temperature at 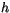 . The quantity
. The quantity 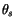 is a measure of
the surface air temperature, which under unstable conditions was given
by
is a measure of
the surface air temperature, which under unstable conditions was given
by
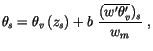 |
(4.470) |
where 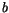 is a constant,
is a constant,
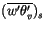 is
the virtual heat flux at the surface,
is
the virtual heat flux at the surface,
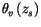 is a
virtual temperature in the atmospheric surface layer (nominally 10 m),
is a
virtual temperature in the atmospheric surface layer (nominally 10 m),
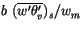 represents a
temperature excess (a measure of the strength of convective thermals
in the lower part of the ABL) and unstable conditions are determined
by
represents a
temperature excess (a measure of the strength of convective thermals
in the lower part of the ABL) and unstable conditions are determined
by
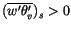 . The quantity
. The quantity
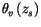 was calculated from the temperature and
moisture of the first model level and of the surface by applying the
procedure in Geleyn [60]. The value of the critical bulk
Richardson number
was calculated from the temperature and
moisture of the first model level and of the surface by applying the
procedure in Geleyn [60]. The value of the critical bulk
Richardson number 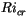 in (4.469), which generally depends
on the vertical resolution of the model, was chosen as
in (4.469), which generally depends
on the vertical resolution of the model, was chosen as 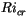 = 0.5
for the CCM2.
= 0.5
for the CCM2.
Vogelezang and Holtslag [178] have recently studied the suitability of this
formulation in the context of field observations, large-eddy
simulations [128], and an
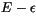 turbulence closure
model [53]. They propose a revised formulation which
combines shear production in the outer region of the boundary layer
with surface friction, where the Richardson number estimate is based
on the differences in wind and virtual temperature between the top of
the ABL and a lower height that is well outside the surface layer (i.e.
20 m - 80 m). In addition to providing more realistic estimates of
boundary layer depth, the revised formulation provides a smoother
transition between stable and neutral boundary layers. Consequently,
CAM 3.0 employs the Vogelezang and Holtslag [178] formulation for estimating the
atmospheric boundary layer height, which can be written as
turbulence closure
model [53]. They propose a revised formulation which
combines shear production in the outer region of the boundary layer
with surface friction, where the Richardson number estimate is based
on the differences in wind and virtual temperature between the top of
the ABL and a lower height that is well outside the surface layer (i.e.
20 m - 80 m). In addition to providing more realistic estimates of
boundary layer depth, the revised formulation provides a smoother
transition between stable and neutral boundary layers. Consequently,
CAM 3.0 employs the Vogelezang and Holtslag [178] formulation for estimating the
atmospheric boundary layer height, which can be written as
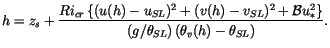 |
(4.471) |
The quantities 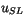 ,
, 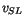 , and
, and
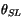 represent the
horizontal wind components and virtual potential temperature just
above the surface layer (nominally 0.1
represent the
horizontal wind components and virtual potential temperature just
above the surface layer (nominally 0.1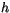 ). In practice, the lowest
model level values for these quantities are used to iteratively
determine
). In practice, the lowest
model level values for these quantities are used to iteratively
determine 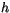 for all stability conditions, where the critical
Richardson number,
for all stability conditions, where the critical
Richardson number, 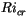 , is assumed to be 0.3. The disposable
parameter
, is assumed to be 0.3. The disposable
parameter 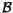 has been experimentally determined to be equal to
100 (see Vogelezang and Holtslag [178]). The computation starts by calculating
the bulk Richardson number
has been experimentally determined to be equal to
100 (see Vogelezang and Holtslag [178]). The computation starts by calculating
the bulk Richardson number 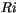 between the level of
between the level of
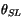 and
subsequent higher levels of the model. Once
and
subsequent higher levels of the model. Once 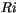 exceeds the critical
value, the value of
exceeds the critical
value, the value of 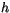 is derived by linear interpolation between the
level with
is derived by linear interpolation between the
level with
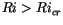 and the level below.
and the level below.
Using the calculated value for 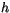 and the surface fluxes, we
calculate the velocity scales, the eddy diffusivities with
(4.467), and the countergradient terms with (4.468), for
each of the transported constituents. Subsequently, the new profiles
for
and the surface fluxes, we
calculate the velocity scales, the eddy diffusivities with
(4.467), and the countergradient terms with (4.468), for
each of the transported constituents. Subsequently, the new profiles
for 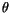 ,
, 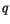 ,
, 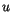 , and
, and 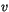 are calculated using an implicit
diffusion formulation.
are calculated using an implicit
diffusion formulation.
The turbulent velocity scale of (4.467) depends primarily on
the relative height 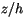 (
(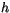 is boundary layer height), and the
stability within the ABL. Here stability is defined with respect to
the surface virtual heat flux
is boundary layer height), and the
stability within the ABL. Here stability is defined with respect to
the surface virtual heat flux
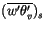 . Secondly, the velocity scales are also
generally dependent on the specific quantity of interest. We will
assume that the velocity scales for mixing of passive scalars and
specific humidity are equal to the one for heat, denoted by
. Secondly, the velocity scales are also
generally dependent on the specific quantity of interest. We will
assume that the velocity scales for mixing of passive scalars and
specific humidity are equal to the one for heat, denoted by 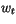 . For
the wind components, the velocity scale is different and denoted by
. For
the wind components, the velocity scale is different and denoted by
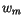 . The specification of
. The specification of 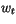 and
and 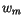 is given in detail by
Troen and Mahrt [174]. Holtslag et al. [75] have rewritten the velocity scale,
in terms of the more widely accepted profile functions of
Dyer [54], and have given a new formulation for very stable
conditions. Below we follow the latter approach.
is given in detail by
Troen and Mahrt [174]. Holtslag et al. [75] have rewritten the velocity scale,
in terms of the more widely accepted profile functions of
Dyer [54], and have given a new formulation for very stable
conditions. Below we follow the latter approach.
For stable (
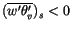 ) and neutral
surface conditions (
) and neutral
surface conditions (
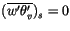 ),
the velocity scale for scalar transport is
),
the velocity scale for scalar transport is
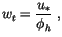 |
(4.472) |
where 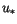 is the friction velocity defined by
is the friction velocity defined by
![$\displaystyle u_\ast = \left[ (\overline{u^\prime w^\prime})_s^2 + (\overline{v^\prime w^\prime})_s^2 \right]^{1/4}.$](img2620.gif) |
(4.473) |
Furthermore, 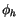 is the dimensionless vertical temperature
gradient given by Dyer [54],
is the dimensionless vertical temperature
gradient given by Dyer [54],
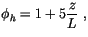 |
(4.474) |
for
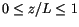 . Here
. Here 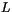 is the Obukhov length, defined by
is the Obukhov length, defined by
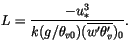 |
(4.475) |
For 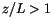 ,
,
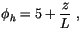 |
(4.476) |
which matches (4.474) for 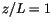 . Equation (4.476) is
a simple means to prevent
. Equation (4.476) is
a simple means to prevent 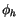 from becoming too large (and
from becoming too large (and 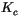 too small) in very stable conditions. In stable conditions, the
exchange coefficients for heat and momentum are often found to be
similar. Therefore we may use
too small) in very stable conditions. In stable conditions, the
exchange coefficients for heat and momentum are often found to be
similar. Therefore we may use 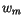 =
=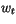 .
.
For unstable conditions
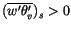 ,
we have that
,
we have that 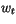 and
and 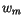 differ in the surface layer
differ in the surface layer
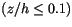 and in the outer layer of the ABL
and in the outer layer of the ABL
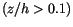 . For the surface
layer,
. For the surface
layer, 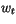 is given by (4.472) with
is given by (4.472) with
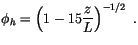 |
(4.477) |
Similarly, 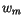 is written as
is written as
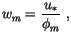 |
(4.478) |
where 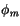 is the dimensionless wind gradient given by
is the dimensionless wind gradient given by
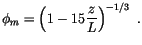 |
(4.479) |
In the surface layer, the scalar flux is normally given by
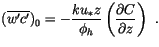 |
(4.480) |
Comparison with (4.466) and (4.467) shows that, in the
surface layer, we should have 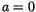 in (4.468) for
consistency.
in (4.468) for
consistency.
For the outer layer, 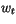 and
and 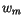 are given by
are given by
is the convective velocity scale. Furthermore, 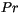 is the turbulent
Prandtl number and
is the turbulent
Prandtl number and 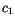 is a constant. The latter is obtained by
evaluating the dimensionless vertical wind gradient
is a constant. The latter is obtained by
evaluating the dimensionless vertical wind gradient 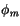 by
(4.479) at the top of the surface layer, as discussed by
Troen and Mahrt [174]. This results in
by
(4.479) at the top of the surface layer, as discussed by
Troen and Mahrt [174]. This results in 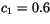 . For very unstable
conditions (
. For very unstable
conditions (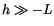 or
or
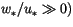 , it can be shown
with (4.481) that
, it can be shown
with (4.481) that 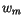 is proportional to 0.85
is proportional to 0.85 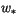 , while
for the neutral case
, while
for the neutral case
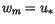 . The turbulent Prandtl number
. The turbulent Prandtl number 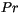
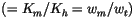 of (4.481) is evaluated from
of (4.481) is evaluated from
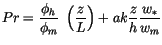 |
(4.484) |
for 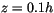 . Equation (4.484) arises from matching
(4.466), (4.467), (4.468), and (4.480) at
the top of the surface layer. As in Troen and Mahrt we assume that
. Equation (4.484) arises from matching
(4.466), (4.467), (4.468), and (4.480) at
the top of the surface layer. As in Troen and Mahrt we assume that
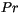 is independent of height in the unstable outer layer. Its value
decreases from
is independent of height in the unstable outer layer. Its value
decreases from 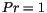 for the neutral case (
for the neutral case (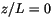 and
and
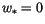 ), to
), to 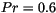 for
for
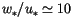 in very unstable
conditions.
in very unstable
conditions.
In very unstable conditions, the countergradient term of
(4.468) approaches
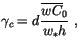 |
(4.485) |
where
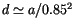 , because for very unstable conditions we
obtain
, because for very unstable conditions we
obtain
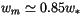 . Since typically
. Since typically
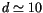 Troen and Mahrt [174], we have
Troen and Mahrt [174], we have 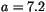 . Similarly, the temperature excess
of (4.470) reads in this limit as
. Similarly, the temperature excess
of (4.470) reads in this limit as
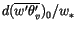 . This leads to
. This leads to 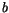 (=
0.85
(=
0.85 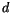 ) = 8.5 in (4.470).
) = 8.5 in (4.470).
Finally, using the velocity scales described above, the flux equation
(4.466) is continuous in relative height (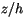 ) and in the
boundary layer stability parameter (
) and in the
boundary layer stability parameter (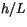 or
or
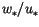 ).
).
In CAM 3.0, as in previous version of the CCM,
(4.448-4.451) are cast in pressure coordinates,
using
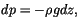 |
(4.486) |
and discretized in a time-split form using an Euler backward time
step. Before describing the numerical solution of the diffusion
equations, we define a compact notation for the discrete equations.
For an arbitrary variable 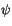 , let a subscript denote a discrete
time level, with current step
, let a subscript denote a discrete
time level, with current step 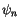 and next step
and next step
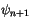 . The
model has
. The
model has 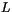 layers in the vertical, with indexes running from top to
bottom. Let
layers in the vertical, with indexes running from top to
bottom. Let 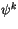 denote a layer midpoint quantity and let
denote a layer midpoint quantity and let
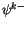 denote the value on the upper interface of layer
denote the value on the upper interface of layer  while
while
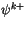 denotes the value on the lower interface. The relevant
quantities, used below, are then:
denotes the value on the lower interface. The relevant
quantities, used below, are then:
Like the continuous equations, the discrete equations are required to
conserve momentum, total energy and constituents. The discrete forms
of (4.448-4.449) are:
For interior interfaces,
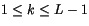 ,
,
Surface fluxes
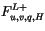 are provided explicitly at time
are provided explicitly at time 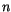 by separate surface models for land, ocean, and sea ice while the top
boundary fluxes are usually
by separate surface models for land, ocean, and sea ice while the top
boundary fluxes are usually
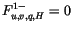 . The turbulent
diffusion coefficients
. The turbulent
diffusion coefficients
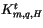 and non-local transport terms
and non-local transport terms
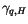 are calculated for time
are calculated for time 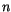 by the turbulence model
described above, which is identical to CCM3. The molecular diffusion
coefficients, described earlier, are only included if the model top
is above
by the turbulence model
described above, which is identical to CCM3. The molecular diffusion
coefficients, described earlier, are only included if the model top
is above 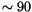 km, in which case nonzero top boundary fluxes may
be included for heat and some constituents.
km, in which case nonzero top boundary fluxes may
be included for heat and some constituents.
The free atmosphere turbulent diffusivities
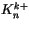 , given by
(4.459-4.465), are discretized as
, given by
(4.459-4.465), are discretized as
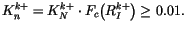 |
(4.492) |
The stability function is:
![$\displaystyle F_c(R_I) = \begin{cases}1/\left(1 + 10 R_I[1+8 R_I]\right) & \tex...
...1ex] \sqrt{1 - 18 R_I} & \text{for} R_I < 0 \text{(unstable)} , \end{cases}$](img2702.gif) |
(4.493) |
The neutral 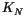 is calculated by
is calculated by
![$\displaystyle {K}_N^{k+} = \ell^2 \frac{\left[\left( \delta^{k+}{u}_{n} \right)^2 + \left( \delta^{k+}{v}_{n} \right)^2 \right]^{1/2}}{\delta^{k+} z_{n}},$](img2704.gif) |
(4.494) |
with 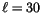 m. The Richardson number in the free atmosphere is
calculated from
m. The Richardson number in the free atmosphere is
calculated from
Similarly to the continuous form (4.456), 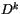 is
determined by separating the kinetic energy change over a time step
into the kinetic energy flux divergence and the kinetic energy
dissipation. The discrete system is required to conserve energy
exactly:
is
determined by separating the kinetic energy change over a time step
into the kinetic energy flux divergence and the kinetic energy
dissipation. The discrete system is required to conserve energy
exactly:
where we have assumed zero boundary fluxes for kinetic energy. This
leads to
According to (4.498), the internal dissipation of kinetic energy
in each layer 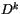 is the average of the dissipation on the bounding
interfaces
is the average of the dissipation on the bounding
interfaces
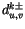 , given by (4.499) and
(4.500). Expanding (4.499) using (4.490)
and recalling that
, given by (4.499) and
(4.500). Expanding (4.499) using (4.490)
and recalling that
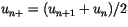 ,
,
![$\displaystyle d_u^{k+} = \frac{\left(g\rho^2 K_m\right)^{k+}}{2\delta^{k+}p} \left[\left(\delta^{k+}u_{n+1}\right)^2 + \delta^{k+}u_{n+1}\delta^{k+}u_{n}\right],$](img2721.gif) |
(4.501) |
for
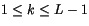 and similarly for
and similarly for 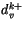 . The discrete
kinetic energy dissipation is not positive definite, because the last
term in (4.501) is the product of the vertical difference of
momentum at two time levels. Although
. The discrete
kinetic energy dissipation is not positive definite, because the last
term in (4.501) is the product of the vertical difference of
momentum at two time levels. Although
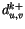 will almost
always be
will almost
always be 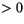 , values
, values 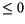 may occur occasionally. The kinetic
energy dissipation at the surface is
may occur occasionally. The kinetic
energy dissipation at the surface is
![$\displaystyle d_{u,v}^{L+} = - \left[(u,v)_{n+1}^L + (u,v)_n^L\right]F_{u,v}^{L+}.$](img2726.gif) |
(4.502) |
Since the surface stress is opposed to the bottom level wind, the
surface layer is heated by the frictional dissipation. However,
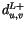 is not guaranteed to be positive, since it involves the
bottom level wind at two time levels.
is not guaranteed to be positive, since it involves the
bottom level wind at two time levels.
Note that it has been assumed that the pressure does not change within
the vertical diffusion, even though there are boundary fluxes of
constituents, including water. This assumption has been made in all
versions of the CCM and is still made in CAM 3.0. This assumption will be
removed in a future version of CAM 3.0, since the implied horizontal
fluxes of dry air, to compensate for the boundary flux of water, cause
implied fluxes of other constituents.
A series of time-split operators is actually defined by
(4.488-4.491) and (4.498-4.500).
Once the diffusivities (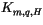 ) and the non-local transport terms
(
) and the non-local transport terms
(
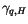 ) have been determined, the solution of
(4.488-4.491), proceeds in several steps.
) have been determined, the solution of
(4.488-4.491), proceeds in several steps.
- update the
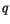 and
and 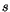 profiles using
profiles using
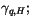
- update the bottom level values of
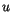 ,
, 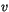 ,
, 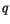 and
and 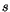 using
the surface fluxes;
using
the surface fluxes;
- invert (4.488) and (4.490) for
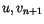 ;
;
- compute
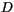 and use to update the
and use to update the 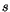 profile;
profile;
- invert (4.488,4.489) and (4.491) for
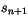 and
and 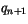 ;
;
Note that since all parameterizations in CAM 3.0 return tendencies
rather than modified profiles, the actual quantities returned by the
vertical diffusion are
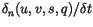 .
.
The non-local transport terms,
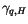 , given by
(4.468), cannot be treated implicitly because they depend on
the surface flux, the boundary layer depth and the velocity scale, but
not explicitly on the profile of the transported quantity. Therefore,
application of
, given by
(4.468), cannot be treated implicitly because they depend on
the surface flux, the boundary layer depth and the velocity scale, but
not explicitly on the profile of the transported quantity. Therefore,
application of 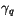 is not guaranteed to give a positive value
for
is not guaranteed to give a positive value
for 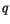 and negative values may not be removed by the subsequent
implicit diffusion step. This problem is not strictly numerical; it
arises under highly non-stationary conditions for which the ABL
formulation is not strictly applicable. In practice, we evaluate
and negative values may not be removed by the subsequent
implicit diffusion step. This problem is not strictly numerical; it
arises under highly non-stationary conditions for which the ABL
formulation is not strictly applicable. In practice, we evaluate
![$\displaystyle q_{n*} = q_n + \frac{g\delta t}{\delta^k p} \delta^k\left[\rho K_{q}^t \gamma_{q}\right]_n$](img2733.gif) |
(4.503) |
and check the 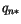 profile for negative values (actually for
profile for negative values (actually for
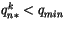 , where
, where 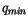 may be
may be 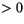 ). If any negative
values are found, we set
). If any negative
values are found, we set
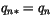 for that constituent profile
(but not for other constituents at the same point).
for that constituent profile
(but not for other constituents at the same point).
Equations (4.488-4.491) constitute a set of four
tridiagonal systems of the form
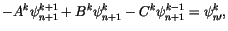 |
(4.504) |
where
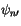 indicates
indicates 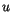 ,
, 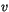 ,
, 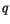 , or
, or 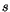 after updating
from time
after updating
from time 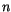 values with the nonlocal and boundary fluxes. The
super-diagonal (
values with the nonlocal and boundary fluxes. The
super-diagonal (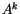 ), diagonal (
), diagonal (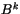 ) and sub-diagonal (
) and sub-diagonal (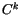 )
elements of (4.504) are:
)
elements of (4.504) are:
The solution of (4.504) has the form
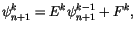 |
(4.508) |
or,
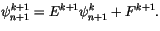 |
(4.509) |
Substituting (4.509) into (4.504),
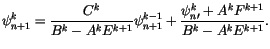 |
(4.510) |
Comparing (4.508) and (4.510), we find
The terms 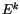 and
and 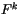 can be determined upward from
can be determined upward from 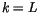 , using
the boundary conditions
, using
the boundary conditions
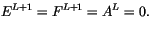 |
(4.513) |
Finally, (4.510) can be solved downward for
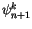 , using the boundary condition
, using the boundary condition
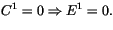 |
(4.514) |
CCM1-3 used the same solution method, but with the order of the
solution reversed, which merely requires writing (4.509)
for
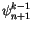 instead of
instead of
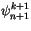 . The order used
here is particularly convenient because the turbulent diffusivities
for heat and all constituents are the same but their molecular
diffusivities are not. Since the terms in
(4.511-4.512) are determined from the bottom
upward, it is only necessary to recalculate
. The order used
here is particularly convenient because the turbulent diffusivities
for heat and all constituents are the same but their molecular
diffusivities are not. Since the terms in
(4.511-4.512) are determined from the bottom
upward, it is only necessary to recalculate 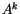 ,
, 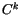 ,
, 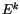 and
and
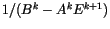 for each constituent within the region where
molecular diffusion is important. Note that including the diffusive
separation term for constituents (which will be in the next version of
CAM 3.0) adds additional terms to the definitions of
for each constituent within the region where
molecular diffusion is important. Note that including the diffusive
separation term for constituents (which will be in the next version of
CAM 3.0) adds additional terms to the definitions of 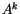 ,
, 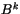 , and
, and
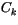 , but does not otherwise change the solution method.
, but does not otherwise change the solution method.
The dry static energy at step 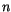 and level
and level  is
is
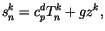 |
(4.515) |
which can be calculated from 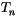 by integrating the hydrostatic
equation using the perfect gas law.
by integrating the hydrostatic
equation using the perfect gas law.
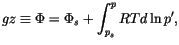 |
(4.516) |
where 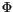 is the geopotential,
is the geopotential, 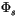 is the geopotential at the
Earth's surface and
is the geopotential at the
Earth's surface and 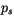 is the surface pressure. A fairly arbitrary
discretization of (4.516) can be represented using a
triangular hydrostatic matrix
is the surface pressure. A fairly arbitrary
discretization of (4.516) can be represented using a
triangular hydrostatic matrix 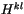 ,
,
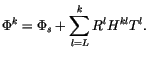 |
(4.517) |
Note that (4.517) is often written in terms of the virtual
temperature
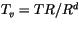 . The apparent gas constant
. The apparent gas constant 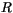 includes
the effect of water vapor and is defined as
includes
the effect of water vapor and is defined as
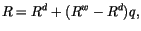 |
(4.518) |
where 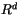 is the apparent gas constant for dry air and
is the apparent gas constant for dry air and 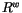 is the
gas constant for water vapor.
is the
gas constant for water vapor.
Using (4.517) in (4.515), we have
The interface geopotential in (4.520) is defined as
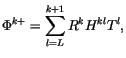 |
(4.521) |
and 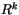 is evaluated from (4.518), using
is evaluated from (4.518), using 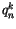 .
Although the correct boundary condition on (4.521) is
.
Although the correct boundary condition on (4.521) is
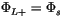 , within the parameterization suite it is usually
sufficient to take
, within the parameterization suite it is usually
sufficient to take
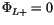 .
.
The definition of the hydrostatic matrix 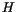 depends on the numerical
method used in the dynamics and is subject to constraints from energy
and mass conservation. The definitions of
depends on the numerical
method used in the dynamics and is subject to constraints from energy
and mass conservation. The definitions of 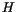 for the three dynamical
methods used in CAM 3.0 are given in the dynamics descriptions.
for the three dynamical
methods used in CAM 3.0 are given in the dynamics descriptions.
After 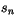 is modified by diabatic heating in a time split process,
the new
is modified by diabatic heating in a time split process,
the new
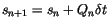 can be converted into
can be converted into 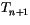 and
and
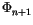 using (4.520):
using (4.520):
with 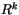 evaluated from using
evaluated from using 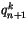 . Once
. Once 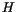 is defined,
(4.521) and (4.523) can be solved for
is defined,
(4.521) and (4.523) can be solved for 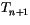 and
and
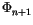 from the bottom up. Since the latter must normally
recalculated if
from the bottom up. Since the latter must normally
recalculated if 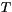 is modified, calculating
is modified, calculating 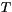 and
and 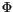 from
from 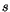 involves the same amount of computation as calculating
involves the same amount of computation as calculating 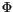 and
and 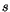 from
from 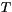 .
.




Next: 4.12 Sulfur Chemistry
Up: 4. Model Physics
Previous: 4.10 Surface Exchange Formulations
Contents
Jim McCaa
2004-06-22
![]() 90 km (0.1 Pa).
90 km (0.1 Pa).
![]() in (4.449) is
determined by forming the equation for total energy from
(4.448-4.449):
in (4.449) is
determined by forming the equation for total energy from
(4.448-4.449):
![]() ), to the
top of the model (
), to the
top of the model (
![]() ):
):
![]() for all
for all ![]() . For unstable conditions
. For unstable conditions ![]() we
choose
we
choose
![]() is modified as in
(4.451):
is modified as in
(4.451):
![]() so (4.466) reduces to a local form with
so (4.466) reduces to a local form with
![]() given by (4.459). Near the top of the ABL we use the
maximum of the values by (4.459) and (4.467), although
(4.467) almost always gives the larger value in practice.
given by (4.459). Near the top of the ABL we use the
maximum of the values by (4.459) and (4.467), although
(4.467) almost always gives the larger value in practice.
![]() , represents
non-local influences on the mixing by turbulence
[48]. As such, this term is small in stable conditions,
and is therefore neglected under these conditions. For unstable
conditions, however, most heat and moisture transport is achieved by
turbulent eddies with sizes on the order of the depth
, represents
non-local influences on the mixing by turbulence
[48]. As such, this term is small in stable conditions,
and is therefore neglected under these conditions. For unstable
conditions, however, most heat and moisture transport is achieved by
turbulent eddies with sizes on the order of the depth ![]() of the
ABL. In such cases, a formulation for
of the
ABL. In such cases, a formulation for ![]() consistent with the
eddy formulation of (4.466) is given by
consistent with the
eddy formulation of (4.466) is given by
![]() . The CCM2 configuration of
this non-local scheme made use of a traditional approach to estimating
the boundary layer depth by assuming a constant value for the bulk
Richardson number across the boundary layer depth so that
. The CCM2 configuration of
this non-local scheme made use of a traditional approach to estimating
the boundary layer depth by assuming a constant value for the bulk
Richardson number across the boundary layer depth so that ![]() was
iteratively determined using
was
iteratively determined using
![]() turbulence closure
model [53]. They propose a revised formulation which
combines shear production in the outer region of the boundary layer
with surface friction, where the Richardson number estimate is based
on the differences in wind and virtual temperature between the top of
the ABL and a lower height that is well outside the surface layer (i.e.
20 m - 80 m). In addition to providing more realistic estimates of
boundary layer depth, the revised formulation provides a smoother
transition between stable and neutral boundary layers. Consequently,
CAM 3.0 employs the Vogelezang and Holtslag [178] formulation for estimating the
atmospheric boundary layer height, which can be written as
turbulence closure
model [53]. They propose a revised formulation which
combines shear production in the outer region of the boundary layer
with surface friction, where the Richardson number estimate is based
on the differences in wind and virtual temperature between the top of
the ABL and a lower height that is well outside the surface layer (i.e.
20 m - 80 m). In addition to providing more realistic estimates of
boundary layer depth, the revised formulation provides a smoother
transition between stable and neutral boundary layers. Consequently,
CAM 3.0 employs the Vogelezang and Holtslag [178] formulation for estimating the
atmospheric boundary layer height, which can be written as
![]() and the surface fluxes, we
calculate the velocity scales, the eddy diffusivities with
(4.467), and the countergradient terms with (4.468), for
each of the transported constituents. Subsequently, the new profiles
for
and the surface fluxes, we
calculate the velocity scales, the eddy diffusivities with
(4.467), and the countergradient terms with (4.468), for
each of the transported constituents. Subsequently, the new profiles
for ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are calculated using an implicit
diffusion formulation.
are calculated using an implicit
diffusion formulation.
![]() (
(![]() is boundary layer height), and the
stability within the ABL. Here stability is defined with respect to
the surface virtual heat flux
is boundary layer height), and the
stability within the ABL. Here stability is defined with respect to
the surface virtual heat flux
![]() . Secondly, the velocity scales are also
generally dependent on the specific quantity of interest. We will
assume that the velocity scales for mixing of passive scalars and
specific humidity are equal to the one for heat, denoted by
. Secondly, the velocity scales are also
generally dependent on the specific quantity of interest. We will
assume that the velocity scales for mixing of passive scalars and
specific humidity are equal to the one for heat, denoted by ![]() . For
the wind components, the velocity scale is different and denoted by
. For
the wind components, the velocity scale is different and denoted by
![]() . The specification of
. The specification of ![]() and
and ![]() is given in detail by
Troen and Mahrt [174]. Holtslag et al. [75] have rewritten the velocity scale,
in terms of the more widely accepted profile functions of
Dyer [54], and have given a new formulation for very stable
conditions. Below we follow the latter approach.
is given in detail by
Troen and Mahrt [174]. Holtslag et al. [75] have rewritten the velocity scale,
in terms of the more widely accepted profile functions of
Dyer [54], and have given a new formulation for very stable
conditions. Below we follow the latter approach.
![]() ) and neutral
surface conditions (
) and neutral
surface conditions (
![]() ),
the velocity scale for scalar transport is
),
the velocity scale for scalar transport is
![]() ,
we have that
,
we have that ![]() and
and ![]() differ in the surface layer
differ in the surface layer
![]() and in the outer layer of the ABL
and in the outer layer of the ABL
![]() . For the surface
layer,
. For the surface
layer, ![]() is given by (4.472) with
is given by (4.472) with
![]() and
and ![]() are given by
are given by
![]() ) and in the
boundary layer stability parameter (
) and in the
boundary layer stability parameter (![]() or
or
![]() ).
).
![]() , given by
(4.459-4.465), are discretized as
, given by
(4.459-4.465), are discretized as
![]() is
determined by separating the kinetic energy change over a time step
into the kinetic energy flux divergence and the kinetic energy
dissipation. The discrete system is required to conserve energy
exactly:
is
determined by separating the kinetic energy change over a time step
into the kinetic energy flux divergence and the kinetic energy
dissipation. The discrete system is required to conserve energy
exactly:
![$\displaystyle {\sum_{k=1}^L \left[(u_{n+1}^k)^2 + (v_{n+1}^k)^2 +
s_{n+1}^k\right]\delta^k p =}$](img2711.gif)
![$\displaystyle \sum_{k=1}^L \left[(u_{n}^k)^2 +
(v_{n}^k)^2 + s_{n}^k\right]\delta^k p + \delta t (F_H^{L+} +
F_H^{1-}),$](img2712.gif)
![]() is the average of the dissipation on the bounding
interfaces
is the average of the dissipation on the bounding
interfaces
![]() , given by (4.499) and
(4.500). Expanding (4.499) using (4.490)
and recalling that
, given by (4.499) and
(4.500). Expanding (4.499) using (4.490)
and recalling that
![]() ,
,
![]() ) and the non-local transport terms
(
) and the non-local transport terms
(
![]() ) have been determined, the solution of
(4.488-4.491), proceeds in several steps.
) have been determined, the solution of
(4.488-4.491), proceeds in several steps.
![]() .
.
![]() , given by
(4.468), cannot be treated implicitly because they depend on
the surface flux, the boundary layer depth and the velocity scale, but
not explicitly on the profile of the transported quantity. Therefore,
application of
, given by
(4.468), cannot be treated implicitly because they depend on
the surface flux, the boundary layer depth and the velocity scale, but
not explicitly on the profile of the transported quantity. Therefore,
application of ![]() is not guaranteed to give a positive value
for
is not guaranteed to give a positive value
for ![]() and negative values may not be removed by the subsequent
implicit diffusion step. This problem is not strictly numerical; it
arises under highly non-stationary conditions for which the ABL
formulation is not strictly applicable. In practice, we evaluate
and negative values may not be removed by the subsequent
implicit diffusion step. This problem is not strictly numerical; it
arises under highly non-stationary conditions for which the ABL
formulation is not strictly applicable. In practice, we evaluate
![]() instead of
instead of
![]() . The order used
here is particularly convenient because the turbulent diffusivities
for heat and all constituents are the same but their molecular
diffusivities are not. Since the terms in
(4.511-4.512) are determined from the bottom
upward, it is only necessary to recalculate
. The order used
here is particularly convenient because the turbulent diffusivities
for heat and all constituents are the same but their molecular
diffusivities are not. Since the terms in
(4.511-4.512) are determined from the bottom
upward, it is only necessary to recalculate ![]() ,
, ![]() ,
, ![]() and
and
![]() for each constituent within the region where
molecular diffusion is important. Note that including the diffusive
separation term for constituents (which will be in the next version of
CAM 3.0) adds additional terms to the definitions of
for each constituent within the region where
molecular diffusion is important. Note that including the diffusive
separation term for constituents (which will be in the next version of
CAM 3.0) adds additional terms to the definitions of ![]() ,
, ![]() , and
, and
![]() , but does not otherwise change the solution method.
, but does not otherwise change the solution method.
![]() and level
and level ![]() is
is
![]() depends on the numerical
method used in the dynamics and is subject to constraints from energy
and mass conservation. The definitions of
depends on the numerical
method used in the dynamics and is subject to constraints from energy
and mass conservation. The definitions of ![]() for the three dynamical
methods used in CAM 3.0 are given in the dynamics descriptions.
for the three dynamical
methods used in CAM 3.0 are given in the dynamics descriptions.
![]() is modified by diabatic heating in a time split process,
the new
is modified by diabatic heating in a time split process,
the new
![]() can be converted into
can be converted into ![]() and
and
![]() using (4.520):
using (4.520):