The general formulation for the open ocean slab model is taken from
Hansen et al. [67], although we have modified it to allow for a
fractional sea ice coverage.
The governing equation for ocean mixed layer temperature ![]() is:
is:
The geographic structure of ocean mixed layer depth ![]() is specified
from Levitus [105]. Monthly mean mixed layer depths are determined
using this dataset's standard measure of salinity
is specified
from Levitus [105]. Monthly mean mixed layer depths are determined
using this dataset's standard measure of salinity
![]() (
(![]() is the density of sea water for a specified
salinity, temperature, and atmospheric pressure) where the equality
is the density of sea water for a specified
salinity, temperature, and atmospheric pressure) where the equality
![]() (surface) = .125 is satisfied on a
(surface) = .125 is satisfied on a
![]() grid. These data are then averaged to the standard CAM 3.0 grid (all
data falling within a CAM 3.0 grid box are equally weighted),
horizontally smoothed 10 times using a 1-2-1 smoother, and capped at
200m (to prevent excessively long adjustment times in coupled
atmosphere ocean experiments). The resulting mixed layer depths in
the tropics are generally shallow (10m-30m) while at high latitudes in
both hemispheres there are large seasonal variations (from 10m up to
the 200m maximum). The annually-averaged geographically-varying mixed
layer depth, which is used for purposes related to energy conservation,
is produced by averaging the monthly mean values.
grid. These data are then averaged to the standard CAM 3.0 grid (all
data falling within a CAM 3.0 grid box are equally weighted),
horizontally smoothed 10 times using a 1-2-1 smoother, and capped at
200m (to prevent excessively long adjustment times in coupled
atmosphere ocean experiments). The resulting mixed layer depths in
the tropics are generally shallow (10m-30m) while at high latitudes in
both hemispheres there are large seasonal variations (from 10m up to
the 200m maximum). The annually-averaged geographically-varying mixed
layer depth, which is used for purposes related to energy conservation,
is produced by averaging the monthly mean values.
The geographic distribution of the internal heat source ![]() is generally
specified on a monthly basis using a control CAM 3.0 integration as
described below. During a SOM numerical integration
is generally
specified on a monthly basis using a control CAM 3.0 integration as
described below. During a SOM numerical integration ![]() is
linearly interpolated between monthly values (taken as mid month) to
the appropriate model time step. The energy fluxes associated with
ice formation and ice melt
(
is
linearly interpolated between monthly values (taken as mid month) to
the appropriate model time step. The energy fluxes associated with
ice formation and ice melt
(![]() and
and ![]() respectively) are explicitly predicted.
respectively) are explicitly predicted.
The net atmosphere-to-ocean heat flux in the absence
of sea ice, ![]() , is defined as:
, is defined as:
The evolution of the mixed-layer temperature field, ![]() , is
evaluated using an explicit forward time step. At iteration n
the required information to advance the forecast include
, is
evaluated using an explicit forward time step. At iteration n
the required information to advance the forecast include
![]() , and
, and ![]() , where
, where
![]() is time invariant and
is time invariant and ![]() is linearly interpolated in time
between prescribed mid-monthly values. It is assumed that the exchange
between the ocean mixed layer and the atmosphere occurs faster than
deep adjustments. Hence, the first adjustment to
is linearly interpolated in time
between prescribed mid-monthly values. It is assumed that the exchange
between the ocean mixed layer and the atmosphere occurs faster than
deep adjustments. Hence, the first adjustment to ![]() is evaluated
as:
is evaluated
as:
The ![]() flux is then adjusted since it is possible (using monthly
specified values of
flux is then adjusted since it is possible (using monthly
specified values of ![]() ) to introduce a non-physical cooling of the
mixed layer when its temperature is at the freezing point. Therefore,
if
) to introduce a non-physical cooling of the
mixed layer when its temperature is at the freezing point. Therefore,
if ![]() and
and
![]() , then
, then
To ensure that the predicted SOM sea ice distribution compares favorably
with the control simulation, and is bounded against unchecked growth
or loss for atmospheric conditions significantly different from
present day, an additional adjustment to ![]() under sea ice is applied:
under sea ice is applied:
| (5.6) |
| (5.7) |
The adjusted ![]() (
(![]() ) is then used to update all ocean
points due to deep ocean heat exchange and transport as:
) is then used to update all ocean
points due to deep ocean heat exchange and transport as:
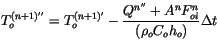 |
(5.8) |
The quantity
![]() is nonzero only if the temperature of the
slab ocean falls below the freezing point:
is nonzero only if the temperature of the
slab ocean falls below the freezing point:
| (5.9) |
| (5.10) |
A renormalization is necessary to ensure energy is conserved when ![]() is adjusted as described above. We distinguish warm ocean as those
points for which
is adjusted as described above. We distinguish warm ocean as those
points for which
![]() C. An adjustment for warm ocean points
is computed after all modifications to
C. An adjustment for warm ocean points
is computed after all modifications to ![]() are completed. Let
are completed. Let ![]() be the original unadjusted
be the original unadjusted ![]() , and let
, and let ![]() be the global (area
weighted) mean. The final (total)
be the global (area
weighted) mean. The final (total) ![]() applied to warm ocean points is:
applied to warm ocean points is:
| (5.11) |