| (6.33) |
This section is only relevant when CAM 3.0 is coupled to a slab ocean. When sea ice is present, only a fraction of the melting potential from heat stored in the ocean actually reaches the ice at the base and side. The melting potential is
| (6.33) |
Usually only a fraction of ![]() is available to melt ice at the
base and side, and these fractions are determined from boundary-layer
theories at the ice-ocean interfaces. However, it is critical that the
sum of the fractions never exceeds one, otherwise ice formation might
become unstable. Hence we compute the upper-limit partitioning of
is available to melt ice at the
base and side, and these fractions are determined from boundary-layer
theories at the ice-ocean interfaces. However, it is critical that the
sum of the fractions never exceeds one, otherwise ice formation might
become unstable. Hence we compute the upper-limit partitioning of
![]() , even though these amounts are rarely
reached. The partitioning assumes
, even though these amounts are rarely
reached. The partitioning assumes ![]() is dominated by shortwave
radiation and that shortwave radiation absorbed in the ocean surface
layer above the mean ice thickness causes side melting and below it
causes basal melting:
is dominated by shortwave
radiation and that shortwave radiation absorbed in the ocean surface
layer above the mean ice thickness causes side melting and below it
causes basal melting:
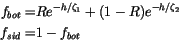 |
(6.34) |
The heat flux for lateral melt is the product of the
vertically-summed, thickness-weighted
energy of melting of snow and ice ![]() with the interfacial melting rate
with the interfacial melting rate ![]() and the total floe
perimeter
and the total floe
perimeter ![]() per unit floe area
per unit floe area ![]() . The interfacial melting rate
is taken from the empirical expression of Maykut and Perovich [124] based on
Marginal Ice Zone Experiment observations:
. The interfacial melting rate
is taken from the empirical expression of Maykut and Perovich [124] based on
Marginal Ice Zone Experiment observations:
![]() ,
where
,
where
![]() m s
m s![]() deg
deg![]() and
and ![]() .
The lead-ice perimeter depends on the ice floe distribution and
geometry. For a mean floe diameter
.
The lead-ice perimeter depends on the ice floe distribution and
geometry. For a mean floe diameter ![]() and number of floes
and number of floes ![]() ,
,
![]() and the floe area
and the floe area
![]() [154].
Thus the heat flux for lateral melt is
[154].
Thus the heat flux for lateral melt is
![]() , so that the actual amount used is:
, so that the actual amount used is:
The heat flux that is actually used by the ice model is then:
| (6.37) |
The net flux exchanged between ocean and ice ![]() also includes
the shortwave flux transmitted to the ocean through sea ice
also includes
the shortwave flux transmitted to the ocean through sea ice
| (6.38) |