



Next: 4.5 Prognostic Condensate and
Up: 4. Model Physics
Previous: 4.3 Evaporation of convective
Contents
4.4 Conversion to and from dry and wet mixing ratios for trace
constituents in the model
There are trade offs in the various options for the representation of trace
constituents 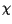 in any general circulation model:
in any general circulation model:
- When the air mass in a model layer is defined to include the
water vapor, it is frequently convenient to represent the quantity
of trace constituent as a ``moist'' mixing ratio
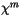 , that is,
the mass of tracer per mass of moist air in the layer. The advantage
of the representation is that one need only multiply the moist
mixing ratio by the moist air mass to determine the tracer air mass.
It has the disadvantage of implicitly requiring a change in
, that is,
the mass of tracer per mass of moist air in the layer. The advantage
of the representation is that one need only multiply the moist
mixing ratio by the moist air mass to determine the tracer air mass.
It has the disadvantage of implicitly requiring a change in 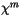 whenever the water vapor
whenever the water vapor 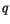 changes within the layer, even if the
mass of the trace constituent does not.
changes within the layer, even if the
mass of the trace constituent does not.
- One can also utilize a ``dry'' mixing ratio
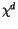 to define the amount
of constituent in a volume of air. This variable does not have the
implicit dependence on water vapor, but does require that the mass
of water vapor be factored out of the air mass itself in order to
calculate the mass of tracer in a cell.
to define the amount
of constituent in a volume of air. This variable does not have the
implicit dependence on water vapor, but does require that the mass
of water vapor be factored out of the air mass itself in order to
calculate the mass of tracer in a cell.
NCAR atmospheric models have historically used a combination of dry
and moist mixing ratios. Physical parameterizations (including
convective transport) have utilized moist mixing ratios. The resolved scale
transport performed in the Eulerian (spectral), and semi-Lagrangian
dynamics use dry mixing ratios, specifically to prevent oscillations
associated with variations in water vapor requiring changes in tracer
mixing ratios. The finite volume dynamics module utilizes moist mixing
ratios, with an attempt to maintain internal consistency between transport of
water vapor and other constituents.
There is no ``right'' way to resolve the requirements associated
with the simultaneous treatment of water vapor, air mass in a layer
and tracer mixing ratios. But the historical treatment significantly
complicates the interpretation of model simulations, and in the latest
version of CAM we have also provided an ``alternate''
representation. That is, we allow the user to specify whether any
given trace constituent is interpreted as a ``dry'' or ``wet'' mixing
ratio through the specification of an ``attribute'' to the constituent
in the physics state structure. The details of the specification are
described in the users manual, but we do identify the interaction
between state quantities here.
At the end of the dynamics update to the model state, the surface
pressure, specific humidity, and tracer mixing ratios are returned to
the model. The physics update then is allowed to update specific
humidity and tracer mixing ratios through a sequence of operator
splitting updates but the surface pressure is not
allowed to evolve. Because there is an explicit relationship
between the surface pressure and the air mass within each layer we
assume that water mass can change within the layer by physical parameterizations but dry air
mass cannot. We have chosen to define the dry air mass in each
layer at the beginning of the physics update as
for column 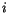 , level
, level  . Note that the specific humidity used is the
value defined at the beginning of the physics update. We define the transformation between dry
and wet mixing ratios to be
We note that the various physical parameterizations that operate on
tracers on the model (convection, turbulent transport, scavenging,
chemistry) will require a specification of the air mass within each
cell as well as the value of the mixing ratio in the cell. We have
modified the model so that it will use the correct value of
. Note that the specific humidity used is the
value defined at the beginning of the physics update. We define the transformation between dry
and wet mixing ratios to be
We note that the various physical parameterizations that operate on
tracers on the model (convection, turbulent transport, scavenging,
chemistry) will require a specification of the air mass within each
cell as well as the value of the mixing ratio in the cell. We have
modified the model so that it will use the correct value of 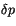 depending on the attribute of the tracer, that is, we use couplets of
depending on the attribute of the tracer, that is, we use couplets of
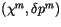 or
or
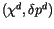 in order to assure
that the process conserves mass appropriately.
in order to assure
that the process conserves mass appropriately.
We note further that there are a number of parameterizations
(e.g. convection, vertical diffusion) that transport species using a
continuity equation in a flux form that can be written generically as
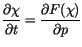 |
(4.108) |
where 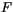 indicates a flux of
indicates a flux of 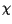 . For example, in convective
transports
. For example, in convective
transports 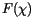 might correspond to
might correspond to 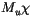 where
where 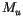 is an
updraft mass flux. In principle one should adjust
is an
updraft mass flux. In principle one should adjust 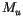 to reflect
the fact that it may be moving a mass of dry air or a mass of moist
air. We assume these differences are small, and well below the
errors required to produce equation 4.108 in the first
place. The same is true for the diffusion coefficients involved in
turbulent transport. All processes using equations of such a form
still satisfy a conservation relationship
to reflect
the fact that it may be moving a mass of dry air or a mass of moist
air. We assume these differences are small, and well below the
errors required to produce equation 4.108 in the first
place. The same is true for the diffusion coefficients involved in
turbulent transport. All processes using equations of such a form
still satisfy a conservation relationship
provided the appropriate 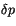 is used in the summation.
is used in the summation.




Next: 4.5 Prognostic Condensate and
Up: 4. Model Physics
Previous: 4.3 Evaporation of convective
Contents
Jim McCaa
2004-06-22
![]() in any general circulation model:
in any general circulation model:
![]() indicates a flux of
indicates a flux of ![]() . For example, in convective
transports
. For example, in convective
transports ![]() might correspond to
might correspond to ![]() where
where ![]() is an
updraft mass flux. In principle one should adjust
is an
updraft mass flux. In principle one should adjust ![]() to reflect
the fact that it may be moving a mass of dry air or a mass of moist
air. We assume these differences are small, and well below the
errors required to produce equation 4.108 in the first
place. The same is true for the diffusion coefficients involved in
turbulent transport. All processes using equations of such a form
still satisfy a conservation relationship
to reflect
the fact that it may be moving a mass of dry air or a mass of moist
air. We assume these differences are small, and well below the
errors required to produce equation 4.108 in the first
place. The same is true for the diffusion coefficients involved in
turbulent transport. All processes using equations of such a form
still satisfy a conservation relationship