



Next: 4.4 Conversion to and
Up: 4. Model Physics
Previous: 4.2 Shallow/Middle Tropospheric Moist
Contents
4.3 Evaporation of convective precipitation
The CAM 3.0 employs a Sundqvist [169] style evaporation of the
convective precipitation as it makes its way to the surface. This
scheme relates the rate at which raindrops evaporate to the local
large-scale subsaturation, and the rate at which convective rainwater
is made available to the subsaturated model layer
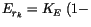 RH RH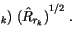 |
(4.103) |
where
RH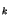 is the relative humidity at level
is the relative humidity at level
 ,
,
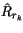 denotes the total rainwater flux at
level
denotes the total rainwater flux at
level  (which can be different from the locally diagnosed rainwater
flux from the convective parameterization, as will be shown
below), the coefficient
(which can be different from the locally diagnosed rainwater
flux from the convective parameterization, as will be shown
below), the coefficient 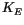 takes the value 0.2
takes the value 0.2 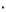 10
10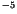 (kg m
(kg m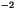 s
s )
)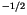 s
s , and the variable
, and the variable 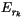 has units of s
has units of s . The
evaporation rate
. The
evaporation rate 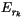 is used to determine a local change in
is used to determine a local change in
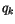 and
and 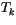 , associated with an evaporative reduction of
, associated with an evaporative reduction of
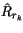 . Conceptually, the evaporation process is invoked
after a vertical profile of
. Conceptually, the evaporation process is invoked
after a vertical profile of 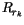 has been evaluated. An
evaporation rate is then computed for the uppermost level of the model
for which
has been evaluated. An
evaporation rate is then computed for the uppermost level of the model
for which
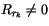 using (4.103), where in this case
using (4.103), where in this case
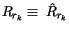 . This rate is used to evaluate an
evaporative reduction in
. This rate is used to evaluate an
evaporative reduction in 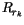 which is then accumulated with the
previously diagnosed rainwater flux in the layer below,
which is then accumulated with the
previously diagnosed rainwater flux in the layer below,
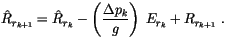 |
(4.104) |
A local increase in the specific humidity 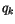 and a local reduction
of
and a local reduction
of 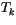 are also calculated in accordance with the net evaporation
are also calculated in accordance with the net evaporation
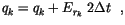 |
(4.105) |
and
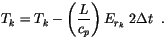 |
(4.106) |
The procedure, (4.103)-(4.106), is then successively
repeated for each model level in a downward direction where the final
convective precipitation rate is that portion of the condensed
rainwater in the column to survive the evaporation process
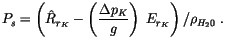 |
(4.107) |
In global annually averaged terms, this evaporation procedure produces
a very small reduction in the convective precipitation rate where the
evaporated condensate acts to moisten the middle and lower
troposphere.




Next: 4.4 Conversion to and
Up: 4. Model Physics
Previous: 4.2 Shallow/Middle Tropospheric Moist
Contents
Jim McCaa
2004-06-22