



Next: 4.7 Parameterization of Cloud
Up: 4. Model Physics
Previous: 4.5 Prognostic Condensate and
Contents
If a layer is unstable with respect to the dry adiabatic lapse rate,
dry adiabatic adjustment is performed. The layer is stable if
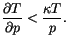 |
(4.160) |
In finite-difference form, this becomes
If there are any unstable layers in the top three model layers, the
temperature is adjusted so that (4.161) is satisfied everywhere
in the column. The variable 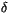 represents a convergence
criterion. The adjustment is done so that sensible heat is conserved,
represents a convergence
criterion. The adjustment is done so that sensible heat is conserved,
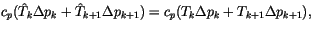 |
(4.163) |
and so that the layer has neutral stability:
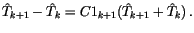 |
(4.164) |
As mentioned above, the hats denote the variables after adjustment.
Thus, the adjusted temperatures are given by
Whenever the two layers undergo dry adjustment, the moisture is
assumed to be completely mixed by the process as well. Thus, the
specific humidity is changed in the two layers in a conserving manner
to be the average value of the original values,
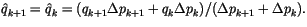 |
(4.168) |
The layers are adjusted iteratively. Initially,
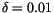 in the stability check (4.161). The column is passed through
from
in the stability check (4.161). The column is passed through
from 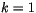 to a user-specifiable lower level (set to 3 in the standard
model configuration) up to 15 times; each time unstable layers are
adjusted until the entire column is stable. If convergence is not
reached by the 15th pass, the convergence criterion is doubled, a
message is printed, and the entire process is repeated. If
to a user-specifiable lower level (set to 3 in the standard
model configuration) up to 15 times; each time unstable layers are
adjusted until the entire column is stable. If convergence is not
reached by the 15th pass, the convergence criterion is doubled, a
message is printed, and the entire process is repeated. If 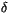 exceeds 0.1 and the column is still not stable, the model stops.
exceeds 0.1 and the column is still not stable, the model stops.
As indicated above, the dry convective adjustment is only applied to
the top three levels of the standard model. The vertical diffusion
provides the stabilizing vertical mixing at other levels. Thus, in
practice, momentum is mixed as well as moisture and potential
temperature in the unstable case.




Next: 4.7 Parameterization of Cloud
Up: 4. Model Physics
Previous: 4.5 Prognostic Condensate and
Contents
Jim McCaa
2004-06-22
![]() represents a convergence
criterion. The adjustment is done so that sensible heat is conserved,
represents a convergence
criterion. The adjustment is done so that sensible heat is conserved,