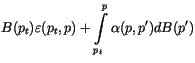 |
(4.229) | ||
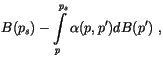 |
(4.230) |
The general method employed for the solution of (4.233) for a
given gas is based on the broad band model approach described by
Kiehl and Briegleb [87] and Kiehl and Ramanathan [93]. This approach is based on the
earlier work of Ramanathan [136]. The broad band approach assumes
that the spectral range of absorption by a gas is limited to a
relatively small range in wavenumber ![]() , and hence can be evaluated
at the band center, i.e.
, and hence can be evaluated
at the band center, i.e.
| (4.242) |
| (4.243) |
The sub-intervals in equation 4.241, in turn, can be reformulated in terms of the absorptance for a given gas and the ``overlap'' transmission factors that multiply this transmission. Note that in the broad band formulation there is an explicit assumption that these two are uncorrelated (see Kiehl and Ramanathan [93]). The specific parameterizations for each of these sub-intervals depends on spectroscopic data particular to a given gas and absorption band for that absorber.
Details of the parameterization for the three major absorbers, H![]() O,
CO
O,
CO![]() and O
and O![]() , are given in Collins et al. [40], Kiehl and Briegleb [87],
and Ramanathan and Dickinson [137], respectively. Therefore, we only provide a
brief description of how these gases are treated in the CAM 3.0. Note
that the original parameterization for H
, are given in Collins et al. [40], Kiehl and Briegleb [87],
and Ramanathan and Dickinson [137], respectively. Therefore, we only provide a
brief description of how these gases are treated in the CAM 3.0. Note
that the original parameterization for H![]() O by Ramanathan and Downey [138]
has been replaced a new formulation in CAM 3.0.
O by Ramanathan and Downey [138]
has been replaced a new formulation in CAM 3.0.
For CO![]()
Water vapor cannot employ the broad-band absorptance method since
H![]() O absorption extends throughout the entire longwave region.
Thus, we cannot factor out the Planck function dependence as in
(4.234). The method of
Collins et al. [40] is used for water-vapor absorptivities and
emissivities. This parameterization replaces the scheme developed by
Ramanathan and Downey [138] used in previous versions of the model. The new
formulation uses the line-by-line radiative transfer model GENLN3
[57] to generate the absorptivities and emissivities for
H
O absorption extends throughout the entire longwave region.
Thus, we cannot factor out the Planck function dependence as in
(4.234). The method of
Collins et al. [40] is used for water-vapor absorptivities and
emissivities. This parameterization replaces the scheme developed by
Ramanathan and Downey [138] used in previous versions of the model. The new
formulation uses the line-by-line radiative transfer model GENLN3
[57] to generate the absorptivities and emissivities for
H![]() O. In this version of GENLN3, the parameters for H
O. In this version of GENLN3, the parameters for H![]() O lines
have been obtained from the HITRAN2k data base [153], and
the continuum is treated with the Clough, Kneizys, and Davies (CKD)
model version 2.4.1 [33]. To generate the absorptivity and
emissivity, GENLN is used to calculate the transmission through
homogeneous atmospheres for H
O lines
have been obtained from the HITRAN2k data base [153], and
the continuum is treated with the Clough, Kneizys, and Davies (CKD)
model version 2.4.1 [33]. To generate the absorptivity and
emissivity, GENLN is used to calculate the transmission through
homogeneous atmospheres for H![]() O lines alone and for H
O lines alone and for H![]() O lines
and continuum. The calculation is done for a five dimensional
parameter space with coordinates equaling the emission temperature,
path temperature, precipitable water, effective relative humidity, and
pressure. The limits for each coordinate span the entire range of
instantaneous values for the corresponding variable from a 1-year
control integration of CAM 3.0. The resulting tables of absorptivity
and emissivity are then read into the model for use in the longwave
calculations. The overlap treatment between water vapor and other
gases is described in Ramanathan and Downey [138].
O lines
and continuum. The calculation is done for a five dimensional
parameter space with coordinates equaling the emission temperature,
path temperature, precipitable water, effective relative humidity, and
pressure. The limits for each coordinate span the entire range of
instantaneous values for the corresponding variable from a 1-year
control integration of CAM 3.0. The resulting tables of absorptivity
and emissivity are then read into the model for use in the longwave
calculations. The overlap treatment between water vapor and other
gases is described in Ramanathan and Downey [138].
The absorptivity and emissivity can be split into terms for the window
and non-window portions of the infrared spectrum. The window is
defined as 800-1200 cm![]() , and the non-window is the remainder
of the spectrum between 20 to 2200 cm
, and the non-window is the remainder
of the spectrum between 20 to 2200 cm![]() . Outside the
mid-infrared window (the so-called non-window region), the H
. Outside the
mid-infrared window (the so-called non-window region), the H![]() O continuum is dominated by the foreign component [34]. The
foreign continuum absorption has the same linear scaling with water
vapor path as line absorption, and thus in the non-window region the
line and continuum absorption are combined in a single expression. In
the window region, where the self-broadened component of the continuum
is dominant, the line and continuum absorption have different scalings
with the amount of water vapor and must be treated separately. The
formalism is identical for the absorptivity and emissivity, and for
brevity only the absorptivity is discussed in detail. The
absorptivity is decomposed into two terms:
O continuum is dominated by the foreign component [34]. The
foreign continuum absorption has the same linear scaling with water
vapor path as line absorption, and thus in the non-window region the
line and continuum absorption are combined in a single expression. In
the window region, where the self-broadened component of the continuum
is dominant, the line and continuum absorption have different scalings
with the amount of water vapor and must be treated separately. The
formalism is identical for the absorptivity and emissivity, and for
brevity only the absorptivity is discussed in detail. The
absorptivity is decomposed into two terms:
| (4.250) |
Let
![]() represent the total non-window absorption for a
homogeneous atmosphere characterized by a set of scaling parameters
represent the total non-window absorption for a
homogeneous atmosphere characterized by a set of scaling parameters
![]() . Scaling theory is a relationship between an inhomogeneous path
and an equivalent homogeneous path with nearly identical line
absorption for the spectral band under consideration [62].
Scaling theory is used to reduce the parameter space of atmospheric
conditions that have to be evaluated. The equivalent pressure,
temperature, and absorber amount are calculated using the standard
Curtis-Godson scaling theory for absorption lines
[61,44]. In addition, we retain explicit dependence
on the emission temperature of the radiation following
Ramanathan and Downey [138], and we introduce dependence on an equivalent
relative humidity. It follows from Curtis-Godson scaling theory that
. Scaling theory is a relationship between an inhomogeneous path
and an equivalent homogeneous path with nearly identical line
absorption for the spectral band under consideration [62].
Scaling theory is used to reduce the parameter space of atmospheric
conditions that have to be evaluated. The equivalent pressure,
temperature, and absorber amount are calculated using the standard
Curtis-Godson scaling theory for absorption lines
[61,44]. In addition, we retain explicit dependence
on the emission temperature of the radiation following
Ramanathan and Downey [138], and we introduce dependence on an equivalent
relative humidity. It follows from Curtis-Godson scaling theory that
In the following expressions, a tilde denotes a parameter derived
using scaling theory for the equivalence between homogeneous and
inhomogeneous atmospheres. The subscript ![]() denotes a parameter which
depends upon the spectral band under consideration. The set of
scaling parameters that determine the total non-window absorption are
labeled:
denotes a parameter which
depends upon the spectral band under consideration. The set of
scaling parameters that determine the total non-window absorption are
labeled:
| (4.252) |
The absorber-weighted path temperature is:
| (4.254) | |||
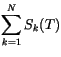 |
(4.257) | ||
![$\displaystyle \left\lbrace\sum_{k=1}^N \left[ S_k(T)
\alpha_k(T)\right]^{1/2} \right\rbrace^2
.$](img1994.gif) |
(4.258) |
| (4.259) |
Although the relative humidity (or H![]() O vapor pressure) is not
included in standard Curtis-Godson scaling theory, it must be treated
as an independent parameter since the vapor pressure determines the
self-broadening of lines and the strength of the self-continuum. The
effective relative humidity
O vapor pressure) is not
included in standard Curtis-Godson scaling theory, it must be treated
as an independent parameter since the vapor pressure determines the
self-broadening of lines and the strength of the self-continuum. The
effective relative humidity
![]() is defined in terms of an
effective H
is defined in terms of an
effective H![]() O specific humidity
O specific humidity
![]() and saturation specific
humidity
and saturation specific
humidity
![]() along the path:
along the path:
The window term
![]() requires a special provision for the different
path parameters for the lines and continuum. Let
requires a special provision for the different
path parameters for the lines and continuum. Let
| (4.266) |
| (4.267) |
The lines-only absorptivity can be written in terms of a line
transmission factor ![]() and an asymptotic absorptivity
and an asymptotic absorptivity
![]() in
the limit of a black-body atmosphere.
in
the limit of a black-body atmosphere.
![]() is a function only of
is a function only of
![]() [138]. The relationship is
[138]. The relationship is
| (4.272) |
In the presence of stratospheric volcanic aerosols, the
expressions for the absorptivity become:
![$\displaystyle A_{nw,\infty}\left[1 - \left(1 - {{\widetilde A}_{nw}(l_{nw}) \over
A_{nw,\infty}} \right) {\cal T}^{nw}_{H_2SO_4} \right]$](img2038.gif) |
|||
| (4.274) |
Methane. The radiative effects of methane are
represented by the last term in (4.241). We re-write this in
terms of the absorptivity due to methane as
Nitrous Oxide. For nitrous oxide there are three
absorption bands of interest: 589, 1168 and 1285 cm![]() bands. The
radiative effects of the 1285 cm
bands. The
radiative effects of the 1285 cm![]() band is given by the last term
in (4.276),
band is given by the last term
in (4.276),
The 1168 cm![]() N
N![]() O band system is represented by the seventh
term on the RHS of (4.241). This term can be re-written as
O band system is represented by the seventh
term on the RHS of (4.241). This term can be re-written as
| Index |
|
||||
| 1 | 750 - 820 | 2.9129e-2 | -1.3139e-4 | 3.0857e-2 | -1.3512e-4 |
| 2 | 820 - 880 | 2.4101e-2 | -5.5688e-5 | 2.3524e-2 | -6.8320e-5 |
| 3 | 880 - 900 | 1.9821e-2 | -4.6380e-5 | 1.7310e-2 | -3.2609e-5 |
| 4 | 900 - 1000 | 2.6904e-2 | -8.0362e-5 | 2.6661e-2 | -1.0228e-5 |
| 5 | 1000 - 1120 | 2.9458e-2 | -1.0115e-4 | 2.8074e-2 | -9.5743e-5 |
| 6 | 1120 - 1170 | 1.9892e-2 | -8.8061e-5 | 2.2915e-2 | -1.0304e-4 |
| Index |
|
||||
| 1 | 750 - 820 | 0.0468556 | 14.4832 | 26.1891 | 0.0261782 |
| 2 | 820 - 880 | 0.0397454 | 4.30242 | 18.4476 | 0.0369516 |
| 3 | 880 - 900 | 0.0407664 | 5.23523 | 15.3633 | 0.0307266 |
| 4 | 900 - 1000 | 0.0304380 | 3.25342 | 12.1927 | 0.0243854 |
| 5 | 1000 - 1120 | 0.0540398 | 0.698935 | 9.14992 | 0.0182932 |
| 6 | 1120 - 1170 | 0.0321962 | 16.5599 | 8.07092 | 0.0161418 |
The final N![]() O band centered at 589 cm
O band centered at 589 cm![]() is represented by the
first term on the RHS of (4.241),
is represented by the
first term on the RHS of (4.241),
CFCs. The effects of both CFC11 and CFC12 are included by using the approach of Ramanathan et al. [139]. Thus, the band absorptance of the CFCs is given by
The contribution by these CFC absorption bands is accounted for by the following terms in (4.241).
For the 798 cm![]() CFC11 band, the absorption effect is given by
the second term on the right hand side of (4.319),
CFC11 band, the absorption effect is given by
the second term on the right hand side of (4.319),
For the 889 cm![]() CFC12 band the absorption is defined by the
second term in (4.321) as
CFC12 band the absorption is defined by the
second term in (4.321) as
Minor CO![]() Bands. There are two minor bands of carbon
dioxide that were added to the CCM3 longwave model. These bands play a
minor role in the present day radiative budget, but are very important
for high levels of CO
Bands. There are two minor bands of carbon
dioxide that were added to the CCM3 longwave model. These bands play a
minor role in the present day radiative budget, but are very important
for high levels of CO![]() , such as during the Archean. The first band
we consider is centered at 961 cm
, such as during the Archean. The first band
we consider is centered at 961 cm![]() . The radiative contribution
of this band is represented by the last term in (4.322),
. The radiative contribution
of this band is represented by the last term in (4.322),
The pressure factor, ![]() , for (4.343) is the same as
defined in (4.338), while the other factors are,
, for (4.343) is the same as
defined in (4.338), while the other factors are,
| (4.350) |
The mixing ratios of methane, nitrous oxide, CFC11 and CFC12 are
specified as zonally averaged quantities. The stratospheric mixing
ratios of these various gases do vary with latitude. This is to mimic
the effects of stratospheric circulation on these tracers. The exact
latitude dependence of the mixing ratio scale height was based on
information from a two dimensional chemical model (S. Solomon,
personal communication). In the troposphere the gases are assumed to
be well mixed,
The clouds in CAM 3.0 are gray bodies with emissivities that depend on cloud phase, condensed water path, and the effective radius of ice particles. The cloud emissivity is defined as
The treatment of cloud overlap follows Collins [38]. The new parameterizations can treat random, maximum, or an arbitrary combination of maximum and random overlap between clouds. This scheme replaces the treatment in CCM3, which was an exact treatment for random overlap of plane-parallel infinitely-thin gray-body clouds. The new method is an exact treatment for arbitrary overlap among the same type of clouds. It is therefore more accurate than the original matrix method of Manabe and Strickler [123] and improved variants of it [135,107].
If longwave scattering is omitted, the upwelling and downwelling longwave fluxes are solutions to uncoupled ordinary differential equations [62]. The emission from clouds is calculated using the Stefan-Boltzmann law applied to the temperatures at the cloud boundaries. The cloud boundaries correspond to the interfaces of the model layers. This approximation greatly simplifies the mathematical form of the flux solutions since the clouds can be treated as boundary conditions for the differential equations. The approximation becomes more accurate as the clouds become more optically thick.
The solutions are formulated in terms of the same conversion of
vertical cloud distributions to binary cloud profiles used for the
shortwave calculations (p. ![[*]](crossref.png) ). First consider
the flux boundary conditions for a maximum-overlap region
). First consider
the flux boundary conditions for a maximum-overlap region ![]() . The
downward flux at the upper boundary of the region is spatially
heterogeneous and has terms contributed by all the binary
configurations above the region. Similarly, the upward flux at the
lower boundary of the region has terms contributed by all the binary
configurations below the region. The fluxes within the region are
area-weighted sums of the fluxes calculated for all possible
combinations of these boundary terms and the cloud configurations
within the region. Fortunately the arithmetic can be simplified
because the solutions to the longwave equations are linear in the
boundary conditions. Therefore the downward (upward) fluxes can be
computed by summing the solutions for each configuration in the region
for a single boundary condition given by the area-averaged fluxes at
the region interfaces denoted by
. The
downward flux at the upper boundary of the region is spatially
heterogeneous and has terms contributed by all the binary
configurations above the region. Similarly, the upward flux at the
lower boundary of the region has terms contributed by all the binary
configurations below the region. The fluxes within the region are
area-weighted sums of the fluxes calculated for all possible
combinations of these boundary terms and the cloud configurations
within the region. Fortunately the arithmetic can be simplified
because the solutions to the longwave equations are linear in the
boundary conditions. Therefore the downward (upward) fluxes can be
computed by summing the solutions for each configuration in the region
for a single boundary condition given by the area-averaged fluxes at
the region interfaces denoted by
![]() (
(
![]() ). The mathematics
is explained in Collins [38]. In the absorptivity-emissivity
method, the boundary conditions are included in the solution using the
emissivity array. In the standard formulation
[138,122] used in CAM 3.0, this array is only defined
for boundary conditions at the top of the model domain for
computational economy. It is not possible to treat arbitrary flux
boundary conditions inside the domain (e.g.,
). The mathematics
is explained in Collins [38]. In the absorptivity-emissivity
method, the boundary conditions are included in the solution using the
emissivity array. In the standard formulation
[138,122] used in CAM 3.0, this array is only defined
for boundary conditions at the top of the model domain for
computational economy. It is not possible to treat arbitrary flux
boundary conditions inside the domain (e.g.,
![]() ) using the
emissivity array. However, the flux boundary conditions
) using the
emissivity array. However, the flux boundary conditions
![]() and
and
![]() are mathematically equivalent to the fluxes from a single
``pseudo'' cloud deck above and below the region, respectively. The
pseudo clouds have unit area and occupy a single model layer. The
vertical positions and emissivities of these clouds are chosen so that
the net area-mean fluxes incident on the top and bottom of the region
equal
are mathematically equivalent to the fluxes from a single
``pseudo'' cloud deck above and below the region, respectively. The
pseudo clouds have unit area and occupy a single model layer. The
vertical positions and emissivities of these clouds are chosen so that
the net area-mean fluxes incident on the top and bottom of the region
equal
![]() and
and
![]() . With the introduction of the pseudo
clouds, the fluxes inside each maximum-overlap region can be
calculated using the standard absorptivity-emissivity formulation.
. With the introduction of the pseudo
clouds, the fluxes inside each maximum-overlap region can be
calculated using the standard absorptivity-emissivity formulation.
The total upward and downward mean fluxes at a layer ![]() within a
maximum-overlap region
within a
maximum-overlap region ![]() are given by:
are given by:
| Stefan-Boltzmann constant | |
| pressure | |
| pressure at top of layer |
|
| pressure at
bottom of layer |
|
| temperature at
pressure |
|
|
|
|
|
|
layer containing
pseudo cloud for
|
|
|
layer containing pseudo
cloud for
|
|
|
emissivity of cloud in layer |
|
|
emissivity of pseudo clouds at
|
|
|
clear-sky absorptivity from pressure |
|
|
downwelling clear-sky flux at layer |
|
|
upwelling clear-sky flux at layer |
|
|
weights for up/downwelling clear-sky
flux at layer |
|
|
weights for up/downwelling flux at
layer |
The downward and upward fluxes for each configuration can be derived
by iterating the longwave equations from TOA and the surface to the
layer ![]() . At each iteration, the solutions are advanced between
successive cloud layers. The final form of the fluxes in
configuration
. At each iteration, the solutions are advanced between
successive cloud layers. The final form of the fluxes in
configuration
![]() is:
is:
The longwave atmospheric heating rate is obtained from
The full calculation of longwave radiation (which includes heating
rates as well as boundary fluxes) is computationally expensive.
Therefore, modifications to the longwave scheme were developed to
improve its efficiency for the diurnal framework. For illustration,
consider the clear-sky fluxes defined in (4.229) and
(4.230). Well over 90% of the longwave computational cost
involves evaluating the absorptivity ![]() and emissivity
and emissivity
![]() . To reduce this computational burden,
. To reduce this computational burden, ![]() and
and
![]() are computed at a user defined frequency that is set to
every 12 model hours in the standard configuration, while longwave
heating rates are computed at the diurnal cycle frequency of once
every model hour.
are computed at a user defined frequency that is set to
every 12 model hours in the standard configuration, while longwave
heating rates are computed at the diurnal cycle frequency of once
every model hour.
Calculation of ![]() and
and ![]() with a period longer than the
evaluation of the longwave heating rates neglects the dependence of
these quantities on variations in temperature, water vapor, and ozone.
However, variations in radiative fluxes due to changes in cloud amount
are fully accounted for at each radiation calculation, which is
regarded to be the dominant effect on diurnal time scales. The
dominant effect on the heating rates of changes in temperature occurs
through the Planck function and is accounted for with this method.
with a period longer than the
evaluation of the longwave heating rates neglects the dependence of
these quantities on variations in temperature, water vapor, and ozone.
However, variations in radiative fluxes due to changes in cloud amount
are fully accounted for at each radiation calculation, which is
regarded to be the dominant effect on diurnal time scales. The
dominant effect on the heating rates of changes in temperature occurs
through the Planck function and is accounted for with this method.
The continuous equations for the longwave calculations require a
sophisticated vertical finite-differencing scheme due to the integral
term
![]() in Equations (4.229)-(4.230). The
reason for the additional care in evaluating this integral arises from
the nonlinear behavior of
in Equations (4.229)-(4.230). The
reason for the additional care in evaluating this integral arises from
the nonlinear behavior of ![]() across a given model layer. For
example, if the flux at interface
across a given model layer. For
example, if the flux at interface ![]() is required, an integral of
the form
is required, an integral of
the form
![]() must be evaluated.
For the nearest layer to level
must be evaluated.
For the nearest layer to level ![]() , the following terms will arise:
, the following terms will arise:
For the upward flux, the nearest layer contribution to the integral is evaluated from
The
![]() are absorptivities
evaluated for the subdivided paths shown in Figure 4.3.
The path-length dependence for the absorptivities arises from the
dependence on the absorptance
are absorptivities
evaluated for the subdivided paths shown in Figure 4.3.
The path-length dependence for the absorptivities arises from the
dependence on the absorptance ![]() [e.g.,
Eq. (4.373)]. Temperatures are known at model levels.
Temperatures at layer interfaces are determined through linear
interpolation in
[e.g.,
Eq. (4.373)]. Temperatures are known at model levels.
Temperatures at layer interfaces are determined through linear
interpolation in ![]() between layer midpoint temperatures. Thus,
between layer midpoint temperatures. Thus,
![]() can be evaluated at all required levels.
The most involved calculation arises from the evaluation of the
fraction of layers shown in Figure 4.3. In general, the
absorptance of a layer can require the evaluation of the following
path lengths:
can be evaluated at all required levels.
The most involved calculation arises from the evaluation of the
fraction of layers shown in Figure 4.3. In general, the
absorptance of a layer can require the evaluation of the following
path lengths:
These path lengths are used extensively in the evaluation of ![]() [137] and
[137] and ![]() [87] and the trace
gases. But path lengths dependent on both
[87] and the trace
gases. But path lengths dependent on both ![]() (i.e.
(i.e. ![]() ) and
) and ![]() (i.e.
(i.e. ![]() ) are also needed in calculating the water-vapor
absorptivity,
) are also needed in calculating the water-vapor
absorptivity,
![]() [138]. To account for
the subdivided layer, a fractional layer amount must be multiplied by
[138]. To account for
the subdivided layer, a fractional layer amount must be multiplied by
![]() and
and ![]() , e.g.
, e.g.
Consider the subdivided path for
![]() ; the total path length
from
; the total path length
from ![]() to
to ![]() for the
for the ![]() path length will be
path length will be
For variables that scale linearly in ![]() , e.g.
, e.g.
![]() ,
the following fractional layer amounts are used:
,
the following fractional layer amounts are used:
These fractional layer amounts are directly analogous to the ![]() but since
but since
![]() is linear in
is linear in ![]() , the squared terms are not
present.
, the squared terms are not
present.
The variable
![]() requires a mean pressure for the
subdivided layer. These are
requires a mean pressure for the
subdivided layer. These are
Finally, fractional layer amounts for ozone path lengths are needed, since ozone is interpolated linearly in physical thickness. These are given by