



Next: 4.9 Parameterization of Longwave
Up: 4. Model Physics
Previous: 4.7 Parameterization of Cloud
Contents
Subsections
With standard name-list settings, both the longwave and shortwave
heating rates are evaluated every model hour. Between hourly
evaluations, the longwave and shortwave fluxes and flux divergences are
held constant.
In CAM 3.0, insolation is computed using the method of
Berger [17]. Using this formulation, the insolation can be
determined for any time within 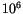 years of 1950 AD. This
facilitates using CAM 3.0 for paleoclimate simulations. The insolation
at the top of the model atmosphere is given by
years of 1950 AD. This
facilitates using CAM 3.0 for paleoclimate simulations. The insolation
at the top of the model atmosphere is given by
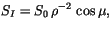 |
(4.174) |
where  is the solar constant,
is the solar constant,  is the solar zenith angle,
and
is the solar zenith angle,
and 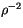 is the distance factor (square of the ratio of mean to
actual distance that depends on the time of year). In the standard
configuration,
is the distance factor (square of the ratio of mean to
actual distance that depends on the time of year). In the standard
configuration,
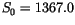 W/m
W/m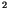 . CAM 3.0 includes a mechanism
for treating the slow variations in the solar constant over the
11-year cycle and during longer secular trends. A time series of
. CAM 3.0 includes a mechanism
for treating the slow variations in the solar constant over the
11-year cycle and during longer secular trends. A time series of 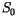 for 1870-2100 based upon Lean et al. [104] is included with the standard
model.
for 1870-2100 based upon Lean et al. [104] is included with the standard
model.
We represent the annual and diurnal cycle of solar insolation with a
repeatable solar year of exactly 365 days and with a mean solar day of
exactly 24 hours, respectively. The repeatable solar year does not
allow for leap years. The expressions defining the annual and diurnal
variation of solar insolation are:
Note that 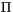 is denoted by
is denoted by 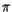 in Berger [17].
in Berger [17].
The hour angle 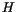 in the expression for
in the expression for 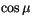 depends on the
calendar day
depends on the
calendar day 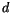 as well as model longitude:
as well as model longitude:
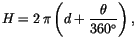 |
(4.180) |
where  = model longitude in degrees starting from Greenwich
running eastward. Note that the calendar day
= model longitude in degrees starting from Greenwich
running eastward. Note that the calendar day  varies continuously
throughout the repeatable year and is updated every model time step.
The values of
varies continuously
throughout the repeatable year and is updated every model time step.
The values of 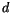 at 0 GMT for January 1 and December 31 are 0 and
364, respectively. This would mean, for example, that a model
calendar day
at 0 GMT for January 1 and December 31 are 0 and
364, respectively. This would mean, for example, that a model
calendar day 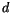 having no fraction (such as 182.00) would refer to
local midnight at Greenwich, and to local noon at the date line
(
having no fraction (such as 182.00) would refer to
local midnight at Greenwich, and to local noon at the date line
(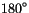 longitude).
longitude).
The obliquity 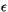 may be approximated by an empirical series
expansion of solutions for the Earth's orbit
may be approximated by an empirical series
expansion of solutions for the Earth's orbit
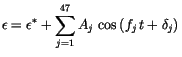 |
(4.181) |
where 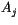 ,
, 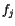 , and
, and 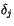 are determined by numerical
fitting. The term
are determined by numerical
fitting. The term
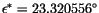 , and
, and 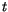 is the time
(in years) relative to 1950 AD.
is the time
(in years) relative to 1950 AD.
Since the series expansion for the eccentricity 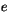 is slowly
convergent, it is computed using
is slowly
convergent, it is computed using
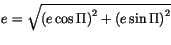 |
(4.182) |
The terms on the right-hand side may also be written as empirical
series expansions:
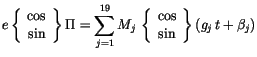 |
(4.183) |
where 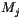 ,
, 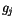 , and
, and 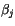 are estimated from numerical
fitting. Once these series have been computed, the longitude of
perihelion
are estimated from numerical
fitting. Once these series have been computed, the longitude of
perihelion 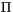 is calculated using
is calculated using
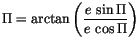 |
(4.184) |
The general precession is given by another empirical series expansion
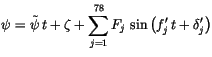 |
(4.185) |
where
 ,
,
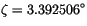 , and
, and 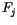 ,
,
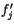 , and
, and 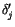 are estimated from the numerical solution for
the Earth's orbit.
are estimated from the numerical solution for
the Earth's orbit.
The calculation of 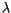 requires first determining two mean
longitudes for the orbit. The mean longitude
requires first determining two mean
longitudes for the orbit. The mean longitude
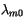 at the
time of the vernal equinox is :
at the
time of the vernal equinox is :
where
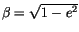 . The mean longitude is
. The mean longitude is
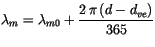 |
(4.187) |
where
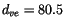 is the calendar day for the vernal equinox at noon
on March 21. The true longitude
is the calendar day for the vernal equinox at noon
on March 21. The true longitude 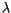 is then given by:
is then given by:
The orbital state used to calculate the insolation is held fixed over
the length of the model integration. This state may be specified in
one of two ways. The first method is to specify a year for computing
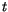 . The value of the year is held constant for the entire length of
the integration. The year must fall within the range of
. The value of the year is held constant for the entire length of
the integration. The year must fall within the range of
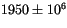 . The second method is to specify the eccentricity factor
. The second method is to specify the eccentricity factor 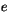 ,
longitude of perihelion
,
longitude of perihelion
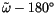 , and obliquity
, and obliquity
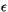 . This set of values is sufficient to specify the complete
orbital state. Settings for AMIP II style integrations under 1995 AD
conditions are
. This set of values is sufficient to specify the complete
orbital state. Settings for AMIP II style integrations under 1995 AD
conditions are
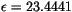 ,
,
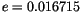 , and
, and
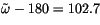 .
.
4.8.2 Formulation of shortwave solution
The 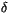 -Eddington approximation of Joseph et al. [80] and
Coakley et al. [35] has been adopted and is described in
Briegleb [27]. This approximation has been shown to simulate
quite well the effects of multiple scattering. The major differences
between the shortwave parameterizations in CCM3 and CAM 3.0 are
-Eddington approximation of Joseph et al. [80] and
Coakley et al. [35] has been adopted and is described in
Briegleb [27]. This approximation has been shown to simulate
quite well the effects of multiple scattering. The major differences
between the shortwave parameterizations in CCM3 and CAM 3.0 are
- the new treatment of cloud vertical overlap [38];
- updated parameterization for near-infrared absorption by water vapor; and
- inclusion of prescribed aerosol data sets for computing shortwave
aerosol radiative forcing.
The solar spectrum is divided into 19 discrete spectral and
pseudo-spectral intervals (7 for
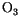 , 1 for the visible,
7 for
, 1 for the visible,
7 for
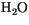 , 3 for
, 3 for
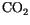 , and 1 for the
near-infrared following Collins [37]). The CAM 3.0 model
atmosphere consists of a discrete vertical set of horizontally
homogeneous layers within which radiative heating rates are to be
specified (see Figure 3.1). Each of these layers is
considered to be a homogeneous combination of several radiatively
active constituents. Solar irradiance, surface reflectivity for
direct and diffuse radiation in each spectral interval, and the cosine
of the solar zenith angle are specified. The surface albedo is
specified in two wavebands (0.2-0.7
, and 1 for the
near-infrared following Collins [37]). The CAM 3.0 model
atmosphere consists of a discrete vertical set of horizontally
homogeneous layers within which radiative heating rates are to be
specified (see Figure 3.1). Each of these layers is
considered to be a homogeneous combination of several radiatively
active constituents. Solar irradiance, surface reflectivity for
direct and diffuse radiation in each spectral interval, and the cosine
of the solar zenith angle are specified. The surface albedo is
specified in two wavebands (0.2-0.7 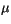 m, and 0.7-5.0
m, and 0.7-5.0 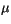 m) and
distinguishes albedos for direct and diffuse incident radiation.
Albedos for ocean surfaces, geographically varying land surfaces, and
sea ice surfaces are distinguished.
m) and
distinguishes albedos for direct and diffuse incident radiation.
Albedos for ocean surfaces, geographically varying land surfaces, and
sea ice surfaces are distinguished.
The method involves evaluating the 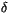 -Eddington solution for the
reflectivity and transmissivity for each layer in the vertical under
clear and overcast conditions. The layers are then combined together,
accounting for multiple scattering between layers, which allows
evaluation of upward and downward spectral fluxes at each interface
boundary between layers. This procedure is repeated for each spectral
or pseudo-spectral interval and binary cloud configuration (see
``Cloud vertical overlap'' below) to accumulate broad band fluxes,
from which the heating rate can be evaluated from flux differences
across each layer. The
-Eddington solution for the
reflectivity and transmissivity for each layer in the vertical under
clear and overcast conditions. The layers are then combined together,
accounting for multiple scattering between layers, which allows
evaluation of upward and downward spectral fluxes at each interface
boundary between layers. This procedure is repeated for each spectral
or pseudo-spectral interval and binary cloud configuration (see
``Cloud vertical overlap'' below) to accumulate broad band fluxes,
from which the heating rate can be evaluated from flux differences
across each layer. The 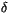 -Eddington scheme is implemented so
that the solar radiation is evaluated once every model hour (in the
standard configuration) over the sunlit portions of the model earth.
-Eddington scheme is implemented so
that the solar radiation is evaluated once every model hour (in the
standard configuration) over the sunlit portions of the model earth.
The 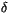 -Eddington approximation allows for gaseous absorption by
-Eddington approximation allows for gaseous absorption by
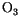 ,
,
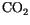 ,
,
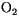 , and
, and
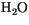 . Molecular scattering and scattering/absorption by
cloud droplets and aerosols are included. With the exception of
. Molecular scattering and scattering/absorption by
cloud droplets and aerosols are included. With the exception of
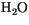 , a summary of the spectral
intervals and the absorption/scattering data used in the formulation
are given in Briegleb [27] and Collins [37]. Diagnostic
cloud amount is evaluated every model hour just prior to the solar
radiation calculation.
, a summary of the spectral
intervals and the absorption/scattering data used in the formulation
are given in Briegleb [27] and Collins [37]. Diagnostic
cloud amount is evaluated every model hour just prior to the solar
radiation calculation.
The absorption by water vapor of sunlight between 1000 and 18000
cm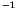 is treated using seven pseudo-spectral intervals. A
constant specific extinction is specified for each interval. These
extinctions have been adjusted to minimize errors in heating rates and
flux divergences relative to line-by-line (LBL) calculations for
reference atmospheres [3] using GENLN3
[57] combined with the radiative transfer solver DISORT2
[163]. The coefficients and weights have the same
properties as a k-distribution method [98], but this
parameterization is essentially an exponential sum fit (e.g.,
Wiscombe and Evans [191]). LBL calculations are performed with the HITRAN2k line database
[153] and the Clough, Kneizys, and Davies (CKD)
model version 2.4.1 [33]. The Rayleigh scattering optical
depths in the seven pseudo-spectral intervals have been changed for
consistency with LBL calculations of the variation of water-vapor
absorption with wavelength. The updated parameterization
increases the absorption of solar radiation by water vapor relative
to the treatment used in CCM and CAM since its introduction by
Briegleb [27].
is treated using seven pseudo-spectral intervals. A
constant specific extinction is specified for each interval. These
extinctions have been adjusted to minimize errors in heating rates and
flux divergences relative to line-by-line (LBL) calculations for
reference atmospheres [3] using GENLN3
[57] combined with the radiative transfer solver DISORT2
[163]. The coefficients and weights have the same
properties as a k-distribution method [98], but this
parameterization is essentially an exponential sum fit (e.g.,
Wiscombe and Evans [191]). LBL calculations are performed with the HITRAN2k line database
[153] and the Clough, Kneizys, and Davies (CKD)
model version 2.4.1 [33]. The Rayleigh scattering optical
depths in the seven pseudo-spectral intervals have been changed for
consistency with LBL calculations of the variation of water-vapor
absorption with wavelength. The updated parameterization
increases the absorption of solar radiation by water vapor relative
to the treatment used in CCM and CAM since its introduction by
Briegleb [27].
For some diagnostic purposes, such as estimating cloud radiative
forcing [94] a clear-sky absorbed solar flux is required.
In CAM 3.0, the clear-sky fluxes and heating rates are computed using
the same vertical grid as the all-sky fluxes. This replaces the
2-layer diagnostic grid used in CCM3.
4.8.3 Aerosol properties and optics
The treatment of aerosols in CAM 3.0 replaces the uniform background
boundary-layer aerosol used in previous versions of CAM and
CCM. The optics for the
globally uniform aerosol were identical to the sulfate aerosols
described by Kiehl and Briegleb [88]. In the visible, the uniform aerosol was
essentially a conservative scatterer.
The new treatment introduces five chemical species of aerosol,
including sea salt, soil dust, black and organic carbonaceous
aerosols, sulfate, and volcanic sulfuric acid.
The new aerosols include two
species, the soil dust and carbonaceous types, which are strongly
absorbing in visible wavelengths and hence increase the shortwave
diabatic heating of the atmosphere.
The three-dimensional time-dependent distributions of the five aerosol
species and the optics for each species are loaded into CAM 3.0 during
the initialization process. This provides considerable flexibility
to:
- Change the speciated aerosol climatology / time-series as
aerosol modeling improves;
- Vary the aerosol distributions for climates different
from present-day conditions;
- Examine the effects of individual aerosol species and arbitrary
combinations of aerosol species; and
- Change aerosol optical properties.
In its present configuration, CAM includes the direct and semi-direct
effects of tropospheric aerosols on shortwave fluxes and heating
rates. The first indirect effect, or
Twomey et al. [175] effect, is not included in the standard version of
CAM 3.0.
4.8.3.2 Description of aerosol climatologies and data sets
The data sets for the tropospheric and stratospheric aerosols are
treated separately in the model.
The annually-cyclic tropospheric aerosol climatology consists of
three-dimensional, monthly-mean distributions of aerosol mass for:
- sulfate from natural and anthropogenic sources;
- sea salt;
- black and organic carbon derived from natural and anthropogenic
sources; and
- soil dust
There are four size categories of dust spanning diameters from
0.01 to 10 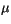 m, and the black and organic
carbon are represented by two tracers each for the hydrophobic (new) and
hydrophilic (aged) components. The climatology therefore contains ten
types of aerosol: sea salt, four size bins of soil dust, sulfate,
new and aged black carbon, and hydrophobic and hydrophilic organic carbon.
m, and the black and organic
carbon are represented by two tracers each for the hydrophobic (new) and
hydrophilic (aged) components. The climatology therefore contains ten
types of aerosol: sea salt, four size bins of soil dust, sulfate,
new and aged black carbon, and hydrophobic and hydrophilic organic carbon.
The climatology is produced using an aerosol assimilation system
[39,41] integrated for present-day conditions. The system
consists of the Model for Atmospheric Chemistry and Transport (MATCH)
[142] and an assimilation of satellite retrievals of aerosol
optical depth. MATCH version 4 is integrated using
the National Centers for Environmental Prediction (NCEP)
meteorological reanalysis at T63 triangular truncation
[83]. The satellite estimates of aerosol optical depth
are from the NOAA Pathfinder II data set [167].
The formulation of the sulfur cycle is described in Barth et al. [12]
and Rasch et al. [143]. The emissions inventory for SO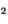 is from
Smith et al. [162].
The sources for mineral dust are based upon
the approach of Zender et al. [196] and Mahowald et al. [120].
The emissions of carbonaceous aerosols include contributions from
biomass burning [113], fossil fuel burning
[42], and a source of
natural organic aerosols resulting from terpene emissions. The
vertical profiles of sea salt are computed from the 10m wind speed
[21].
is from
Smith et al. [162].
The sources for mineral dust are based upon
the approach of Zender et al. [196] and Mahowald et al. [120].
The emissions of carbonaceous aerosols include contributions from
biomass burning [113], fossil fuel burning
[42], and a source of
natural organic aerosols resulting from terpene emissions. The
vertical profiles of sea salt are computed from the 10m wind speed
[21].
The monthly-mean mass path for each aerosol species in each layer is
computed in units of kg/m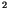 . During the initialization of CAM 3.0,
the climatology is temporally interpolated from monthly-mean to mid-month
values. At each CAM 3.0 time step, the mid-month values bounding the
current time step are vertically interpolated onto the pressure grid
of CAM 3.0 and then time interpolated to the current time step. The
interpolation scheme in CAM 3.0 preserves the aerosol masses for each
species to 1 part in 10
. During the initialization of CAM 3.0,
the climatology is temporally interpolated from monthly-mean to mid-month
values. At each CAM 3.0 time step, the mid-month values bounding the
current time step are vertically interpolated onto the pressure grid
of CAM 3.0 and then time interpolated to the current time step. The
interpolation scheme in CAM 3.0 preserves the aerosol masses for each
species to 1 part in 10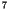 relative to the climatology, and it is
guaranteed to yield positive definite mass-mixing ratios for all
aerosols.
relative to the climatology, and it is
guaranteed to yield positive definite mass-mixing ratios for all
aerosols.
The stratospheric volcanic aerosols are treated using a single species
in the standard model. Zonal variations in the stratospheric mass
loading are omitted. The volcanic input consists of the monthly-mean
masses in units of kg/m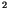 on an arbitrary meridional and vertical
grid. The time series for the recent past is based upon
Ammann et al. [2] following Stenchikov et al. [166].
on an arbitrary meridional and vertical
grid. The time series for the recent past is based upon
Ammann et al. [2] following Stenchikov et al. [166].
The three intrinsic optical properties stored for each of the eleven
aerosol types are specific extinction, single scattering albedo, and
asymmetry parameter. These properties are computed on the band
structure of CAM 3.0 using Chandrasekhar weighting with spectral solar
insolation. The aerosol types affected by hygroscopic growth are
sulfate, sea salt, and hydrophilic organic carbon. In previous
versions of CCM and CAM 3.0, the relative humidity was held constant in
calculations of hygroscopic growth at 80%. In CAM 3.0, the actual
profiles of relative humidity computed from the model state each
radiation time step are used in the calculation.
The optics for black and organic carbon are identical to the optics
for soot and water-soluble aerosols in the Optical Properties of
Aerosols and Clouds (OPAC) data set [69]. The optics for
dust are derived from Mie calculations for the size distribution
represented by each size bin [196]. The Mie
calculations for sulfate assume that it is comprised of ammonium
sulfate with a log-normal size distribution. The dry size parameters
are a median radius of 0.05 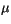 m and a geometric standard deviation
of 2.0. The optical properties in the seven H
m and a geometric standard deviation
of 2.0. The optical properties in the seven H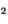 O pseudo-spectral
intervals are averaged consistently with LBL calculations of the
variation of water-vapor absorption with wavelength. This averaging
technique preserves the cross correlations among the spectral
variation of solar insolation, water vapor absorption, and the aerosol
optical properties.
The volcanic stratospheric aerosols are assumed
to be comprised of 75% sulfuric acid and 25% water. The log-normal
size distribution has an effective radius of 0.426
O pseudo-spectral
intervals are averaged consistently with LBL calculations of the
variation of water-vapor absorption with wavelength. This averaging
technique preserves the cross correlations among the spectral
variation of solar insolation, water vapor absorption, and the aerosol
optical properties.
The volcanic stratospheric aerosols are assumed
to be comprised of 75% sulfuric acid and 25% water. The log-normal
size distribution has an effective radius of 0.426 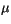 m and a
standard deviation of 1.25.
m and a
standard deviation of 1.25.
The bulk formulae of Cess [30] are used to combine the optical
properties of the individual aerosol species into a single set of bulk
aerosol extinctions, single-scattering albedos, and asymmetry parameters
for each layer.
CAM 3.0 includes a mechanism to scale the masses of each aerosol
species by user-selectable factors at runtime. These factors are
global, time-independent constants. This provides the flexibility to
consider the climate effects of an arbitrary combination of the
aerosol species in the climatology. It also facilitates simulation of
climates different from present-day conditions for which the only
information available is the ratio of globally averaged aerosol
emissions or atmospheric loadings. A mechanism to scale the
carbonaceous aerosols with a time-dependent unitless factor has been
included to facilitate realistic simulations of the recent past.
CAM 3.0 also includes a run-time option for computing a diagnostic set of
shortwave fluxes with an arbitrary combination of aerosols multiplied
with a separate set of user-selectable scale factors. This option
can be used to compute, for example, the aerosol radiative forcing
relative to an atmosphere containing no aerosols.
The diagnostic fields produced the aerosol calculation include the
column-integrated optical depth and column-averaged single-scattering
albedo, asymmetry parameter, and forward scattering parameter (in the
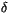 -Eddington approximation) for each aerosol species and
spectral interval. These fields are only computed for illuminated grid
points, and for non-illuminated points the fields are set to zero.
The fraction of the time that a given grid point is illuminated is
also recorded. Time
averages of, for example, the optical depth can be obtained by
dividing the time-averaged optical depths in the history files by the
corresponding daylit fractions.
-Eddington approximation) for each aerosol species and
spectral interval. These fields are only computed for illuminated grid
points, and for non-illuminated points the fields are set to zero.
The fraction of the time that a given grid point is illuminated is
also recorded. Time
averages of, for example, the optical depth can be obtained by
dividing the time-averaged optical depths in the history files by the
corresponding daylit fractions.
The option of introducing a globally uniform background sulfate aerosol
is retained, although by default the optical depth of this aerosol
is set to zero. Its optical properties are computed using the same
sulfate optics as are used for the aerosol climatology. However, for
consistency with the uniform aerosol in previous versions of CAM 3.0 and CCM3,
the relative humidity used to compute hygroscopic growth is set to 80%.
4.8.4.1 Parameterization of effective radius
Observational studies have shown a distinct difference between
maritime, polar, and continental effective cloud drop size, 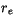 , for
warm clouds. For this reason, CAM 3.0 differentiates between the cloud
drop effective radius for clouds diagnosed over maritime and
continental regimes [89], and over pristine surfaces (sea
ice, snow covered land). Over the ocean, the cloud drop
effective radius for liquid water clouds,
, for
warm clouds. For this reason, CAM 3.0 differentiates between the cloud
drop effective radius for clouds diagnosed over maritime and
continental regimes [89], and over pristine surfaces (sea
ice, snow covered land). Over the ocean, the cloud drop
effective radius for liquid water clouds, 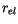 , is specified
to be 14
, is specified
to be 14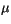 m. Over sea ice, where we presume pristine conditions,
m. Over sea ice, where we presume pristine conditions,
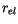 is also specified to be 14
is also specified to be 14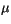 m. Over land masses
m. Over land masses 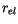 is determined using
is determined using
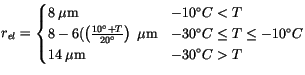 |
(4.189) |
This does not necessarily correspond to the range over which the cloud
ice fraction increases from 0 to 1. In addition, 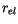 ramps
linearly toward the pristine value of 14
ramps
linearly toward the pristine value of 14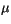 m as water equivalent
snow depth over land goes from 0 to 0.1 m.
m as water equivalent
snow depth over land goes from 0 to 0.1 m.
An ice particle effective radius, 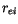 , is also diagnosed by CAM 3.0.
Following Kristjánsson and Kristiansen [97], the effective radius for ice clouds
is now a function only of temperature, as shown in Figure 4.2.
, is also diagnosed by CAM 3.0.
Following Kristjánsson and Kristiansen [97], the effective radius for ice clouds
is now a function only of temperature, as shown in Figure 4.2.
Figure 4.2:
Ice effective radius and terminal
velocity. Top, ice effective radius versus
temperature. Bottom, ice velocity versus radius (left) and temperature (right);
the Stokes terminal velocity is solid and the actual velocity is dashed.
|
|
For cloud scattering and absorption, the radiative parameterization of
Slingo [160] for liquid water droplet clouds is employed. In this
parameterization, the optical properties of the cloud droplets are
represented in terms of the prognosed cloud water path (CWP, in units
of kg m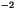 ) and effective radius
) and effective radius
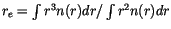 , where
, where 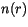 is the cloud drop size distribution as a
function of radius
is the cloud drop size distribution as a
function of radius 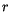 .
.
Cloud radiative properties explicitly account for the phase of
water. For shortwave radiation we use the following generalization of
the expression used by Slingo [160] for liquid water clouds. The
cloud liquid optical properties (extinction optical depth, single
scattering albedo, asymmetry parameter and forward scattering
parameter) for each spectral interval are defined as
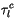 |
 |
![$\displaystyle CWP\left[ a_l^{i}+\frac{b_l^i}{r_{el}} \right] \left(
1-f_{ice} \right)$](img1763.gif) |
(4.190) |
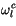 |
 |
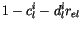 |
(4.191) |
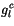 |
 |
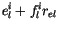 |
(4.192) |
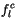 |
 |
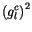 |
(4.193) |
where superscript 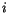 denotes spectral interval. The spectral
intervals and coefficients for liquid water are defined in
Slingo [160].
denotes spectral interval. The spectral
intervals and coefficients for liquid water are defined in
Slingo [160].
The radiative properties of ice cloud are defined
by
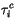 |
 |
![$\displaystyle CWP\left[ a_i^i+ \frac{b_i^i}{r_{ei}} \right] f_{ice}$](img1771.gif) |
(4.194) |
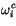 |
 |
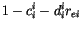 |
(4.195) |
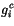 |
 |
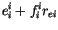 |
(4.196) |
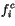 |
 |
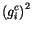 |
(4.197) |
where the subscript 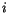 denotes ice radiative properties. The values
for the coefficients
denotes ice radiative properties. The values
for the coefficients 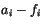 are based on the results of Ebert and Curry [55]
for the four pseudo-spectral intervals (.25-.69
are based on the results of Ebert and Curry [55]
for the four pseudo-spectral intervals (.25-.69 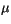 m,
.69-1.19
m,
.69-1.19 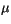 m, 1.19-2.38
m, 1.19-2.38 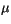 m, and 2.38-4.00
m, and 2.38-4.00 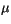 m) employed in
the CAM 3.0 shortwave radiation model. Note that when
m) employed in
the CAM 3.0 shortwave radiation model. Note that when
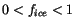 ,
then the combination of these expressions in (4.204 -
4.207) represent the radiative properties for a mixed phase
cloud.
,
then the combination of these expressions in (4.204 -
4.207) represent the radiative properties for a mixed phase
cloud.
4.8.5 Cloud vertical overlap
The treatment of cloud vertical overlap follows Collins [38].
The overlap parameterization is designed to reproduce calculations
based upon the independent column approximation (ICA). The differences
between the results from the new parameterization and ICA are governed
by a set of parameters in the shortwave code
(Table 4.1 on page ![[*]](crossref.png) and
section 4.8.9). The differences can be made
arbitrarily small with appropriate settings of these parameters. The
current parameter settings represent a compromise between
computational cost and accuracy.
and
section 4.8.9). The differences can be made
arbitrarily small with appropriate settings of these parameters. The
current parameter settings represent a compromise between
computational cost and accuracy.
The new parameterizations can treat random, maximum, or an arbitrary
combination of maximum and random overlap between clouds. The type of
overlap is specified with the same two variables for the longwave and
shortwave calculations. These variables are the number of
random-overlap interfaces between adjacent groups of
maximally-overlapped layers and a vector of the pressures at each of
the interfaces. The specification of the overlap is completely
separated from the radiative calculations, and if necessary the type
of overlap can change at each grid cell or time step.
4.8.5.1 Conversion of cloud amounts to binary cloud
profiles
The algorithm for cloud overlap first converts the vertical profile of
partial cloudiness into an equivalent collection of binary cloud
configurations. Let
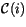 be the fractional amount of cloud in
layer
be the fractional amount of cloud in
layer 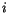 in a profile with
in a profile with 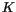 layers. The index
layers. The index 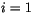 corresponds
to the top of the model atmosphere and
corresponds
to the top of the model atmosphere and 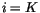 corresponds to the
layer adjacent to the surface. Let
corresponds to the
layer adjacent to the surface. Let  be the number of
maximally-overlapped regions in the column separated by random-overlap
boundaries. If the entire column is maximally overlapped, then
be the number of
maximally-overlapped regions in the column separated by random-overlap
boundaries. If the entire column is maximally overlapped, then 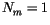 , and if the entire column is randomly overlapped, then
, and if the entire column is randomly overlapped, then 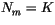 .
Each region
.
Each region 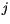 includes all layers
includes all layers 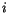 between
between
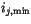 and
and
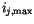 .
Within each region, identify the
.
Within each region, identify the 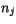 unique, non-zero cloud amounts
and sort them into a descending list
unique, non-zero cloud amounts
and sort them into a descending list
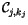 with
with
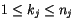 .
Note than in CAM 3.0, cloud amounts are not allowed to be identically
equal to 1. It is convenient to define
.
Note than in CAM 3.0, cloud amounts are not allowed to be identically
equal to 1. It is convenient to define
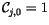 and
and
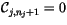 . By construction
. By construction
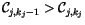 for
for
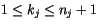 .
.
The binary cloud configurations are defined in terms of the sorted
cloud amounts. The number of unique cloud binary configurations in
region 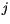 is
is 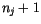 . The
. The
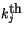 binary cloud
configuration
binary cloud
configuration
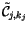 in region
in region 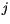 is given by
is given by
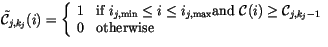 |
(4.198) |
with
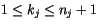 . The fractional area of this configuration
is
. The fractional area of this configuration
is
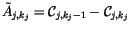 |
(4.199) |
The binary cloud configurations for each maximum-overlap region can be
combined into cloud configurations for the entire column. Because of
the random overlap boundaries between regions, the number of column
configurations is
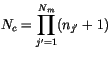 |
(4.200) |
Let
![$ \tilde{\cfrac }[k_1,\ldots,k_{N_m}]$](img1801.gif) represent the column configuration with
represent the column configuration with
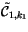 in region 1,
in region 1,
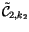 in
region 2, etc. The vertical profile of binary cloud elements is given
by:
in
region 2, etc. The vertical profile of binary cloud elements is given
by:
 = \sum_{j' = 1}^{N_m} \tilde{\cfrac }_{{j'},k_{j'}}(i)$](img1804.gif) |
(4.201) |
The area of this configuration is
![$\displaystyle \tilde{A}[k_1,\ldots,k_{N_m}] = \prod_{j' = 1}^{N_m} \tilde{A}_{{j'},k_{j'}}$](img1805.gif) |
(4.202) |
The cloud overlap for radiative calculations in CAM 3.0 is
maximum-random (M/R). Clouds in adjacent layers are maximally
overlapped, and groups of clouds separated by one or more clear layers
are randomly overlapped. The two overlap parameters input to the
radiative calculations are the number of random-overlap interfaces,
which equals 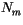 , and a vector of pressures
, and a vector of pressures 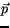 at each
random-overlap interface. These parameters are determined for each
grid cell at each radiation time step. Suppose there are
at each
random-overlap interface. These parameters are determined for each
grid cell at each radiation time step. Suppose there are 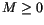 groups of vertically contiguous clouds in a given grid cell. The
first parameter
groups of vertically contiguous clouds in a given grid cell. The
first parameter
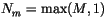 . Let
. Let 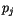 represent the pressure
at the bottom interface of each group of contiguous clouds, and let
represent the pressure
at the bottom interface of each group of contiguous clouds, and let
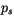 denote the surface pressure. Both
denote the surface pressure. Both 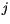 and
and 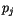 increase from
the top of the model downward. Then
increase from
the top of the model downward. Then
![$\displaystyle \vec p = \left\{\begin{array}{ll} \left[ p_s \right] & \hbox{if $...
...p_1, \>\ldots\>, p_{M-1}, p_s \right] &
\hbox{if $M \ge 2$}
\end{array} \right.$](img1810.gif) |
|
|
(4.203) |
For diagnostic purposes, the CAM 3.0 calculates three levels of cloud
fraction assuming the same maximum-random overlap as in the radiative
calculations. These diagnostics, denoted as low, middle, and high
cloud, are bounded by the pressure levels 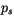 to 700 mb, 700 mb to
400 mb, and 400 mb to the model top.
to 700 mb, 700 mb to
400 mb, and 400 mb to the model top.
The solution for the shortwave fluxes is calculated by determining all
possible arrangements of binary clouds which are consistent with the
vertical profile of partial cloudiness, the overlap assumption, and
the parameters for accelerating the solution (Table 4.1
and section 4.8.9).
The shortwave radiation within each of these configurations is
calculated using the same 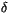 -Eddington solver introduced in CCM3
[27]. The all-sky fluxes and heating rates for the
original profile of partial cloudiness are calculated as weighted sums
of the corresponding quantities from each configuration. The weights
are equal to the horizontal fractional area occupied by each
configuration. The number of configurations is given by
eqn. (4.200), and the area of each configuration is given
by eqn. (4.202). There are two steps in the calculations:
first, the calculation of the cloud-free and overcast radiative
properties for each layer, and second the combination of these
properties using the adding method to calculate fluxes. These two
processes are described below.
-Eddington solver introduced in CCM3
[27]. The all-sky fluxes and heating rates for the
original profile of partial cloudiness are calculated as weighted sums
of the corresponding quantities from each configuration. The weights
are equal to the horizontal fractional area occupied by each
configuration. The number of configurations is given by
eqn. (4.200), and the area of each configuration is given
by eqn. (4.202). There are two steps in the calculations:
first, the calculation of the cloud-free and overcast radiative
properties for each layer, and second the combination of these
properties using the adding method to calculate fluxes. These two
processes are described below.
Details of the implementation are as follows. The CAM 3.0 model
atmosphere is divided into 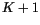 layers in the vertical; an extra top
layer (with index 0, above the
layers in the vertical; an extra top
layer (with index 0, above the 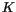 layers specified by CAM 3.0) is
added. This extra layer prevents excessive heating in the top layer
when the top pressure is not very low; also, as the model does not
specify absorber properties above its top layer, the optical
properties of the top layer must be used for the extra layer. In
CAM 3.0, clear-sky and all-sky solar fluxes are calculated and output
for the top of model (TOM) at layer 1 and the top of atmosphere (TOA)
corresponding to layer 0. The TOM fluxes are used to compute the
model energetic balance, and the TOA fluxes are output for diagnostic
comparison against satellite measurements. The provision of both sets
of fluxes is new in CAM 3.0. Layers are assumed to be horizontally and
vertically homogeneous for each model grid point and are bounded
vertically by layer interfaces. For each spectral band, upward and
downward fluxes are computed on the layer interfaces (which include
the surface and top interface). The spectral fluxes are summed and
differenced across layers to evaluate the solar heating rate. The
following discussion refers to each of the spectral intervals.
layers specified by CAM 3.0) is
added. This extra layer prevents excessive heating in the top layer
when the top pressure is not very low; also, as the model does not
specify absorber properties above its top layer, the optical
properties of the top layer must be used for the extra layer. In
CAM 3.0, clear-sky and all-sky solar fluxes are calculated and output
for the top of model (TOM) at layer 1 and the top of atmosphere (TOA)
corresponding to layer 0. The TOM fluxes are used to compute the
model energetic balance, and the TOA fluxes are output for diagnostic
comparison against satellite measurements. The provision of both sets
of fluxes is new in CAM 3.0. Layers are assumed to be horizontally and
vertically homogeneous for each model grid point and are bounded
vertically by layer interfaces. For each spectral band, upward and
downward fluxes are computed on the layer interfaces (which include
the surface and top interface). The spectral fluxes are summed and
differenced across layers to evaluate the solar heating rate. The
following discussion refers to each of the spectral intervals.
In general, several constituents absorb and/or scatter in each
homogeneous layer (e.g. cloud, aerosol, gases...). Every constituent
is defined in terms of a layer extinction optical depth 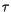 , single
scattering albedo
, single
scattering albedo 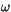 , asymmetry parameter
, asymmetry parameter 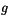 , and the forward
scattering fraction
, and the forward
scattering fraction 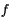 . To define bulk layer properties, the
combination formulas of Cess [30] are used:
. To define bulk layer properties, the
combination formulas of Cess [30] are used:
where the sums are over all constituents.
The 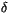 -Eddington solution for each layer requires scaled
properties for
-Eddington solution for each layer requires scaled
properties for 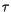 ,
, 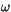 ,
, 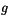 , given by the expressions:
, given by the expressions:
The scaling accounts for the scattering effects of the strong forward
peak in particle scattering. The 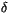 -Eddington nonconservative
(
-Eddington nonconservative
(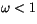 ) solutions for each layer for direct radiation at cosine
zenith angle
) solutions for each layer for direct radiation at cosine
zenith angle 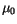 are (following the notation of Coakley et al. [35]:
are (following the notation of Coakley et al. [35]:
where 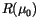 ,
, 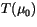 are the layer reflectivity and
transmissivity to direct radiation respectively, and
are the layer reflectivity and
transmissivity to direct radiation respectively, and
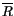 ,
,
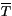 are the layer reflectivity and transmissivity to diffuse
radiation respectively. It should be noted that in some cases of
small but nonzero
are the layer reflectivity and transmissivity to diffuse
radiation respectively. It should be noted that in some cases of
small but nonzero 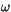 , the diffuse reflectivity can be negative.
For these cases,
, the diffuse reflectivity can be negative.
For these cases,
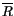 is set to 0, which produces negligible
impact on fluxes and the heating rate. Note that in the new overlap
scheme, these properties are computed separately for the clear and
cloud-filled portions of each layer [38].
is set to 0, which produces negligible
impact on fluxes and the heating rate. Note that in the new overlap
scheme, these properties are computed separately for the clear and
cloud-filled portions of each layer [38].
To combine layers, it is assumed that radiation, once scattered, is
diffuse and isotropic (including from the surface). For an arbitrary
layer 1 (or combination of layers with radiative properties
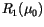 ,
,
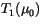 ,
,
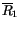 ,
,
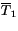 )
overlaying layer 2 (or combination of layers with radiative properties
)
overlaying layer 2 (or combination of layers with radiative properties
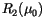 ,
,
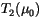 , and
, and
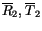 ), the
combination formulas for direct and diffuse radiation incident from
above are:
), the
combination formulas for direct and diffuse radiation incident from
above are:
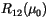 |
 |
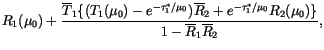 |
(4.220) |
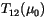 |
 |
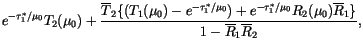 |
(4.221) |
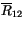 |
 |
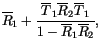 |
(4.222) |
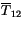 |
 |
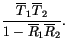 |
(4.223) |
Note that the transmissions for each layer (
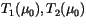 )
and for the combined layers
)
and for the combined layers
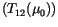 are total transmissions,
containing both direct and diffuse transmission. Note also that the
two layers (or combination of layers), once combined, are no longer a
homogeneous system.
are total transmissions,
containing both direct and diffuse transmission. Note also that the
two layers (or combination of layers), once combined, are no longer a
homogeneous system.
To combine the layers over the entire column, two passes are made
through the layers, one starting from the top and proceeding downward,
the other starting from the surface and proceeding upward. The result
is that for every interface, the following combined reflectivities and
transmissivities are available:
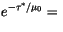 |
direct beam transmission from top-of-atmosphere to the |
|
| |
interface (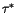 is the scaled optical depth from top-of-atmosphere is the scaled optical depth from top-of-atmosphere |
|
| |
to the interface), |
|
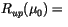 |
reflectivity to direct solar radiation of entire atmosphere |
|
| |
below the interface, |
|
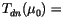 |
total transmission to direct solar radiation incident from above |
|
| |
to entire atmosphere above the interface, |
|
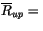 |
reflectivity of atmosphere below the interface to diffuse |
|
| |
radiation from above, |
|
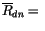 |
reflectivity of atmosphere above the interface to diffuse |
|
| |
radiation from below. |
|
With these quantities, the upward and downward fluxes at every
interface can be computed. For example, the upward flux would be the
directly transmitted flux (
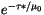 ) times the reflection
of the entire column below the interface to direct radiation
(
) times the reflection
of the entire column below the interface to direct radiation
(
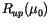 ), plus the diffusely transmitted radiation from above
that reaches the interface (
), plus the diffusely transmitted radiation from above
that reaches the interface (
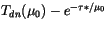 )
times the reflectivity of the entire atmosphere below the interface to
diffuse radiation from above (
)
times the reflectivity of the entire atmosphere below the interface to
diffuse radiation from above (
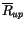 ), all times a factor
that accounts for multiple reflections at the interface. A similar
derivation of the downward flux is straightforward. The resulting
expressions for the upward and downward flux are:
), all times a factor
that accounts for multiple reflections at the interface. A similar
derivation of the downward flux is straightforward. The resulting
expressions for the upward and downward flux are:
Note that in the new overlap scheme, the calculation of the combined
reflectivities, transmissions, and fluxes at layer interfaces are
computed for each binary cloud configuration, subject to techniques
for significantly accelerating these calculations (below)
[38].
If two or more configurations of binary clouds are identical between
TOA and a particular interface, then
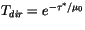 ,
,
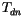 , and
, and
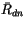 are also identical at that interface. The adding
method is applied once and the three radiative quantities are copied
to all the identical configurations. This process is applied at each
interface by constructing a binary tree of identical cloud
configurations starting at TOA down to the surface. A similar method
is used for
are also identical at that interface. The adding
method is applied once and the three radiative quantities are copied
to all the identical configurations. This process is applied at each
interface by constructing a binary tree of identical cloud
configurations starting at TOA down to the surface. A similar method
is used for 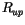 and
and
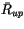 , which are calculated using the adding
method starting the surface and continuing up to a particular
interface. The copying of identical radiative properties reduces the
number of calculations of
, which are calculated using the adding
method starting the surface and continuing up to a particular
interface. The copying of identical radiative properties reduces the
number of calculations of 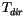 ,
, 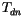 , and
, and
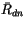 by 62% and the
number of calculations of
by 62% and the
number of calculations of 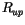 and
and
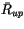 by 21% in CAM 3.0 with M/R
overlap.
by 21% in CAM 3.0 with M/R
overlap.
4.8.9 Methods for reducing the number of binary cloud
configurations
The computational cost of the shortwave code has two components: a
fixed cost for computing the radiative properties of each layer under
clear and overcast conditions, and a variable cost for applying the
adding method for each column configuration
![$ \tilde{\cfrac }[k_1,\ldots,k_{N_m}]$](img1801.gif) . The
variable component can be reduced by omitting configurations which
contribute small terms in the shortwave fluxes. Several mechanisms
for selecting configurations for omission have been included in the
parameterization. The parameters that govern the selection process
are described in Table 4.1.
. The
variable component can be reduced by omitting configurations which
contribute small terms in the shortwave fluxes. Several mechanisms
for selecting configurations for omission have been included in the
parameterization. The parameters that govern the selection process
are described in Table 4.1.
Table 4.1:
Parameters for Decreasing Number of SW
Calculations.
| Parameter |
Symbol |
Definition |
Value in CAM 3.0 |
|
|
| cldmin |
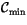 |
Minimum cloud area |
0 |
. | |
|
| cldeps |
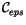 |
Minimum cloud area difference |
0 |
. | |
|
| areamin |
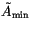 |
Minimum configuration area |
0 |
. | 01 |
|
| nconfgmax |
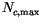 |
Maximum # of configurations |
15 |
. | |
|
Any combination of the selection conditions may be imposed. If the
parameter
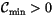 , cloud layers with
, cloud layers with
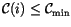 are
identified as cloud-free layers. The configurations including these
clouds are excluded from the flux calculations. If the parameter
are
identified as cloud-free layers. The configurations including these
clouds are excluded from the flux calculations. If the parameter
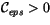 , the cloud
amounts are discretized by
, the cloud
amounts are discretized by
![$\displaystyle \cfrac (i) \rightarrow \left[{\cfrac (i) \over \cfrac _{eps}}\right] \cfrac _{eps}$](img1891.gif) |
(4.226) |
where ![$ [x]$](img1892.gif) represents rounding to the nearest integer less than
represents rounding to the nearest integer less than 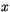 .
This reduces the number of unique, non-zero cloud amounts
.
This reduces the number of unique, non-zero cloud amounts 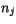 in
each maximum-overlap region
in
each maximum-overlap region 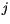 . For example, if
. For example, if
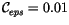 , then
two cloud amounts are distinguished only if they differ by more than
0.01. If the parameter
, then
two cloud amounts are distinguished only if they differ by more than
0.01. If the parameter
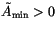 , only configurations with
, only configurations with
![$ \tilde{A}[k_1,\ldots,k_{N_m}] \ge \tilde{A}_{\min}$](img1895.gif) are retained in the calculation. The fluxes
and heating rates are normalized by the area of these configurations:
are retained in the calculation. The fluxes
and heating rates are normalized by the area of these configurations:
![$\displaystyle \tilde{A}_{tot}= \sum_{k_1 = 1}^{n_1 + 1} \cdots \sum_{k_{N_m} = ...
..._{N_m}] \;\;\theta\left(\tilde{A}[k_1,\ldots,k_{N_m}] - \tilde{A}_{\min}\right)$](img1896.gif) |
(4.227) |
where 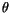 is the Heaviside
function. In CAM 3.0,
is the Heaviside
function. In CAM 3.0,
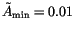 . Finally, if the number of
configurations
. Finally, if the number of
configurations
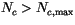 , then only the
, then only the
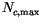 configurations
with the largest values of
configurations
with the largest values of
![$ \tilde{A}[k_1,\ldots,k_{N_m}]$](img1899.gif) are retained. This is
equivalent to setting
are retained. This is
equivalent to setting
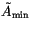 so that the largest
so that the largest
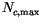 configurations are selected. The fluxes and heating rates are
normalized by
configurations are selected. The fluxes and heating rates are
normalized by
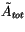 calculated with this value of
calculated with this value of
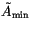 . With the
current cloud parameterizations in CAM 3.0 and with
. With the
current cloud parameterizations in CAM 3.0 and with
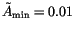 , the
mean and RMS
, the
mean and RMS 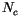 are approximately 5.
are approximately 5.
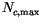 is set to 15, or 2
standard deviations above the mean
is set to 15, or 2
standard deviations above the mean 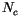 . Only 5% of cloud
configurations in CAM 3.0 have
. Only 5% of cloud
configurations in CAM 3.0 have
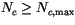 . The errors of the
solutions relative to ICA are relatively insensitive to
. The errors of the
solutions relative to ICA are relatively insensitive to
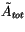 [38].
[38].
The upward and downward spectral fluxes at each interface are summed
to evaluate the spectrally integrated fluxes, then differenced to
produce the solar heating rate,
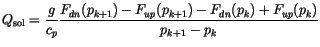 |
(4.228) |
which is added to the nonlinear term 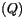 in the thermodynamic
equation.
in the thermodynamic
equation.




Next: 4.9 Parameterization of Longwave
Up: 4. Model Physics
Previous: 4.7 Parameterization of Cloud
Contents
Jim McCaa
2004-06-22
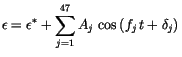
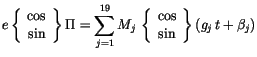
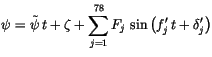
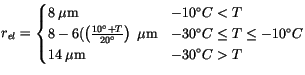
![\includegraphics[width=4.25in,angle=0]{figures/ice}](img1758.gif)
![[*]](crossref.png)
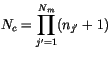
 = \sum_{j' = 1}^{N_m} \tilde{\cfrac }_{{j'},k_{j'}}(i)$](img1804.gif)
![$\displaystyle \tilde{A}[k_1,\ldots,k_{N_m}] = \prod_{j' = 1}^{N_m} \tilde{A}_{{j'},k_{j'}}$](img1805.gif)
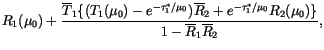
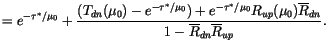
![$\displaystyle \tilde{A}_{tot}= \sum_{k_1 = 1}^{n_1 + 1} \cdots \sum_{k_{N_m} = ...
..._{N_m}] \;\;\theta\left(\tilde{A}[k_1,\ldots,k_{N_m}] - \tilde{A}_{\min}\right)$](img1896.gif)