The albedo depends upon spectral band, snow thickness, ice thickness
and surface temperature. Snow and ice spectral albedos (visible
![]() , wavelengths
, wavelengths
![]() and near-infrared
and near-infrared ![]() , wavelengths
, wavelengths
![]() ) are distinguished, as both snow and ice spectral
reflectivities are significantly higher in the
) are distinguished, as both snow and ice spectral
reflectivities are significantly higher in the ![]() band than in the
band than in the
![]() band. This two-band separation represents the basic spectral
dependence. The near-infrared spectral structure, with generally
decreasing reflectivity with increasing wavelength [56] is
ignored. The zenith angle dependence of snow and ice is ignored
[63,56], and hence there is no distinction between
downwelling direct and diffuse shortwave radiation. The approximations
made for the albedo are further described by Briegleb et al. [28].
band. This two-band separation represents the basic spectral
dependence. The near-infrared spectral structure, with generally
decreasing reflectivity with increasing wavelength [56] is
ignored. The zenith angle dependence of snow and ice is ignored
[63,56], and hence there is no distinction between
downwelling direct and diffuse shortwave radiation. The approximations
made for the albedo are further described by Briegleb et al. [28].
Here we ignore the dependence of snow albedo on age, but retain the melting/non-melting distinction and thickness dependence. Dry snow spectral albedos are:
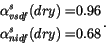 |
(6.7) |
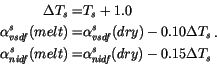 |
(6.8) |
For bare non-melting sea ice thicker than 0.5 m, as is the case for all sea ice prescribed in CAM 3.0, the albedos are
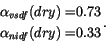 |
(6.9) |
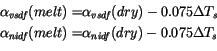 |
(6.10) |
The horizontal fraction of surface covered with snow is assumed to be
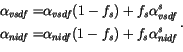 |
(6.12) |