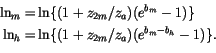Next: 6.5 Ice to Ocean
Up: 6. Sea Ice Thermodynamics
Previous: 6.3 Snow and Ice
Contents
Atmospheric states and downwelling fluxes, along with surface states and
properties, are used to compute atmosphere-ice shortwave and longwave fluxes,
stress, sensible and latent heat fluxes. Surface states are temperature 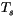 and
albedos
and
albedos
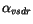 ,
,
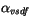 ,
,
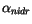 ,
,
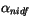 (see section 6.3), while surface properties are longwave emissivity
(see section 6.3), while surface properties are longwave emissivity
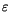 and aerodynamic roughness
and aerodynamic roughness 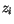 (note that these properties in
general vary with ice thickness, but are here assumed constant). Additionally,
certain flux temperature derivatives required for the ice temperature calculation
are computed, as well as a reference diagnostic surface air temperature.
(note that these properties in
general vary with ice thickness, but are here assumed constant). Additionally,
certain flux temperature derivatives required for the ice temperature calculation
are computed, as well as a reference diagnostic surface air temperature.
The following formulas are for the absorbed
shortwave fluxes and upwelling longwave flux:
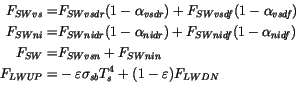 |
(6.13) |
for 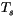 in Kelvin and
in Kelvin and
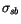 denotes the Stefan-Boltzmann
constant. The downwelling shortwave flux and albedos distinguish
between visible (
denotes the Stefan-Boltzmann
constant. The downwelling shortwave flux and albedos distinguish
between visible (
 ), near-infrared (
), near-infrared (
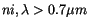 ), direct (
), direct (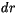 ) and diffuse (
) and diffuse (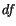 ) radiation for
each category. Note that the upwelling longwave flux has a reflected
component from the downwelling longwave whenever
) radiation for
each category. Note that the upwelling longwave flux has a reflected
component from the downwelling longwave whenever
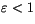 .
.
For stress components 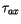 and
and 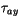 and sensible and
latent heat fluxes the following bulk formulas are used [29]:
and sensible and
latent heat fluxes the following bulk formulas are used [29]:
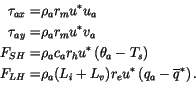 |
(6.14) |
The quantities from the lowest layer of the atmosphere include wind
components 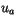 and
and 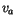 , the density of air
, the density of air 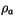 , the potential
temperature
, the potential
temperature 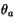 , and the specific humidity
, and the specific humidity 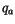 . The surface
saturation specific humidity is
. The surface
saturation specific humidity is
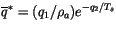 |
(6.15) |
where the values of 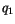 and
and 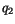 were kindly supplied by Xubin Zeng
of the University of Arizona. The specific heat of the air in the
lowest layer is evaluated from
were kindly supplied by Xubin Zeng
of the University of Arizona. The specific heat of the air in the
lowest layer is evaluated from
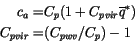 |
(6.16) |
where specific heat of dry air and water vapor are 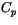 and
and
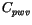 , respectively. Values for the exchange coefficients
for momentum, sensible and latent heat
, respectively. Values for the exchange coefficients
for momentum, sensible and latent heat 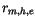 and the friction
velocity
and the friction
velocity 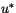 require further consideration.
require further consideration.
The bulk formulas are based on Monin-Obukhov similarity theory. Among
boundary layer scalings, this is the most well tested
[99]. It is based on the assumption that in the surface
layer (typically the lowest tenth of the atmospheric boundary layer),
but away from the surface roughness elements, only the distance from
the boundary and the surface kinematic fluxes are important in the
turbulent exchange. The fundamental turbulence scales that are formed
from these quantities are the friction velocity 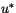 , the
temperature and moisture fluctuations
, the
temperature and moisture fluctuations
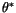 and
and 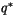 respectively, and the Monin-Obukhov length scale
respectively, and the Monin-Obukhov length scale 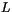 :
:
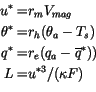 |
(6.17) |
with
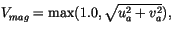 |
(6.18) |
to prevent zero or small fluxes under quiescent wind conditions,
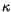 is von Karman's constant (0.4), and
is von Karman's constant (0.4), and 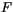 is the buoyancy
flux, defined as:
is the buoyancy
flux, defined as:
![$\displaystyle F = \frac{u^\ast} {g} \left[ \frac{\theta^\ast}{\theta_{v}} + \frac{q^\ast}{z_v^{-1}+q_a} \right]$](img2974.gif) |
(6.19) |
with g the gravitational acceleration and the virtual potential temperature
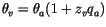 where
where
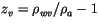 .
.
Similarity theory holds that the vertical gradients of mean horizontal
wind, potential temperature and specific humidity are universal
functions of stability parameter
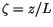 , where
, where 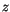 is height
above the surface (
is height
above the surface (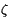 is positive for a stable surface layer and
negative for an unstable surface layer). These universal similarity
functions are determined from observations in the atmospheric boundary
layer [73] though no single form is widely accepted.
Integrals of the vertical gradient relations result in the familiar
logarithmic mean profiles, from which the exchange coefficients can be
defined, where
is positive for a stable surface layer and
negative for an unstable surface layer). These universal similarity
functions are determined from observations in the atmospheric boundary
layer [73] though no single form is widely accepted.
Integrals of the vertical gradient relations result in the familiar
logarithmic mean profiles, from which the exchange coefficients can be
defined, where
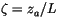 :
:
![\begin{equation*}\null \vcenter{\openup\jot \mathsurround=0pt \ialign{\strut\hf...
...\chi_h(\zeta)\right]\right\}^{-1}\cr r_{e} = & r_{h} \cr\crcr}} \end{equation*}](img2979.gif) |
(6.20) |
with the neutral coefficient
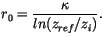 |
(6.21) |
The flux profile functions (integrals of the similarity functions
mentioned above) for momentum 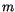 and heat/moisture
and heat/moisture 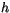 are:
are:
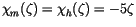 |
(6.22) |
for stable conditions (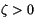 ). For unstable conditions (
). For unstable conditions (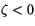 ):
):
The stability parameter 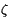 is a function of the turbulent scales and
thus the fluxes, so an iterative solution is necessary. The coefficients are
initialized with their neutral value
is a function of the turbulent scales and
thus the fluxes, so an iterative solution is necessary. The coefficients are
initialized with their neutral value 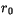 , from which the turbulent scales,
stability, and then flux profile functions can be evaluated. This order is
repeated for five iterations to ensure convergence to an acceptable solution.
, from which the turbulent scales,
stability, and then flux profile functions can be evaluated. This order is
repeated for five iterations to ensure convergence to an acceptable solution.
The surface temperature derivatives required by the ice temperature calculation are
evaluated as:
where the small temperature dependencies of 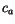 , the exchange coefficients
, the exchange coefficients 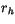 and
and
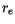 and velocity scale
and velocity scale 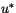 are ignored.
are ignored.
For diagnostic purposes, an air temperature (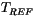 ) at the reference height of
) at the reference height of
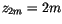 is computed, making use of the stability and momentum/sensible heat exchange
coefficients. Defining
is computed, making use of the stability and momentum/sensible heat exchange
coefficients. Defining
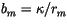 , and
, and
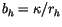 , we have:
, we have:
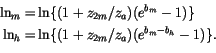 |
(6.29) |
For stable conditions (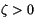 )
)
where 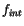 is bounded by 0 and 1. The resulting reference temperature is:
is bounded by 0 and 1. The resulting reference temperature is:
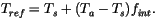 |
(6.32) |




Next: 6.5 Ice to Ocean
Up: 6. Sea Ice Thermodynamics
Previous: 6.3 Snow and Ice
Contents
Jim McCaa
2004-06-22
![]() and
albedos
and
albedos
![]() ,
,
![]() ,
,
![]() ,
,
![]() (see section 6.3), while surface properties are longwave emissivity
(see section 6.3), while surface properties are longwave emissivity
![]() and aerodynamic roughness
and aerodynamic roughness ![]() (note that these properties in
general vary with ice thickness, but are here assumed constant). Additionally,
certain flux temperature derivatives required for the ice temperature calculation
are computed, as well as a reference diagnostic surface air temperature.
(note that these properties in
general vary with ice thickness, but are here assumed constant). Additionally,
certain flux temperature derivatives required for the ice temperature calculation
are computed, as well as a reference diagnostic surface air temperature.
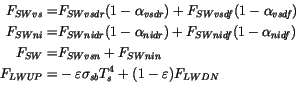
![]() and
and ![]() and sensible and
latent heat fluxes the following bulk formulas are used [29]:
and sensible and
latent heat fluxes the following bulk formulas are used [29]:
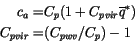
![]() , the
temperature and moisture fluctuations
, the
temperature and moisture fluctuations
![]() and
and ![]() respectively, and the Monin-Obukhov length scale
respectively, and the Monin-Obukhov length scale ![]() :
:
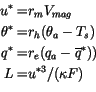
![]() , where
, where ![]() is height
above the surface (
is height
above the surface (![]() is positive for a stable surface layer and
negative for an unstable surface layer). These universal similarity
functions are determined from observations in the atmospheric boundary
layer [73] though no single form is widely accepted.
Integrals of the vertical gradient relations result in the familiar
logarithmic mean profiles, from which the exchange coefficients can be
defined, where
is positive for a stable surface layer and
negative for an unstable surface layer). These universal similarity
functions are determined from observations in the atmospheric boundary
layer [73] though no single form is widely accepted.
Integrals of the vertical gradient relations result in the familiar
logarithmic mean profiles, from which the exchange coefficients can be
defined, where
![]() :
:
![\begin{equation*}\null \vcenter{\openup\jot \mathsurround=0pt \ialign{\strut\hf...
...\chi_h(\zeta)\right]\right\}^{-1}\cr r_{e} = & r_{h} \cr\crcr}} \end{equation*}](img2979.gif)
![]() is a function of the turbulent scales and
thus the fluxes, so an iterative solution is necessary. The coefficients are
initialized with their neutral value
is a function of the turbulent scales and
thus the fluxes, so an iterative solution is necessary. The coefficients are
initialized with their neutral value ![]() , from which the turbulent scales,
stability, and then flux profile functions can be evaluated. This order is
repeated for five iterations to ensure convergence to an acceptable solution.
, from which the turbulent scales,
stability, and then flux profile functions can be evaluated. This order is
repeated for five iterations to ensure convergence to an acceptable solution.
![]() ) at the reference height of
) at the reference height of
![]() is computed, making use of the stability and momentum/sensible heat exchange
coefficients. Defining
is computed, making use of the stability and momentum/sensible heat exchange
coefficients. Defining
![]() , and
, and
![]() , we have:
, we have: