



Next: 6.3 Snow and Ice
Up: 6. Sea Ice Thermodynamics
Previous: 6.1 Basic assumptions
Contents
The method for computing the surface turbulent heat and radiative
exchange, evaporative flux, and surface drag is integrally coupled
with the formulation of heat transfer through the sea ice and snow.
The equation governing vertical heat transfer in the ice and snow,
which allows for internal absorption of penetrating solar radiation,
is
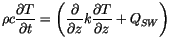 |
(6.1) |
where 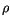 is the density,
is the density, 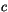 is the heat capacity,
is the heat capacity, 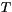 is the
temperature,
is the
temperature,  is the thermal conductivity,
is the thermal conductivity, 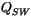 is
shortwave radiative heating,
is
shortwave radiative heating, 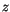 is the vertical coordinate, and
is the vertical coordinate, and 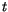 is time. Note that
is time. Note that 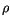 ,
, 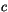 , and
, and  differ for snow and sea ice,
and also the latter two depend on temperature and salinity within the
sea ice to account for the behavior of brine pockets.
differ for snow and sea ice,
and also the latter two depend on temperature and salinity within the
sea ice to account for the behavior of brine pockets.
The boundary condition for the heat equation at the surface is
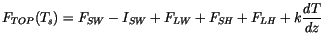 |
(6.2) |
where 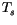 is the surface temperature,
is the surface temperature, 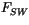 is the absorbed
shortwave flux,
is the absorbed
shortwave flux, 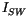 is the shortwave flux that penetrates into
the ice interior,
is the shortwave flux that penetrates into
the ice interior, 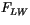 is the net longwave flux,
is the net longwave flux, 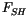 is the
sensible heat flux, and
is the
sensible heat flux, and 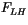 is the latent heat flux. All fluxes
are taken as positive down. If
is the latent heat flux. All fluxes
are taken as positive down. If
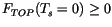 , then the surface
is assumed to be melting and a temperature boundary conditions (i.e.,
, then the surface
is assumed to be melting and a temperature boundary conditions (i.e.,
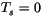 ) is used for the upper boundary with Eq. 6.1.
However if
) is used for the upper boundary with Eq. 6.1.
However if
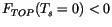 in Eq. 6.2, then the surface
is assumed to be freezing and a flux boundary condition is used for
Eq. 6.1, and Eqs. 6.1 and 6.2 are
solved simultaneously with
in Eq. 6.2, then the surface
is assumed to be freezing and a flux boundary condition is used for
Eq. 6.1, and Eqs. 6.1 and 6.2 are
solved simultaneously with
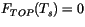 in the latter.
in the latter.
Snow melt and accumulation is computed from
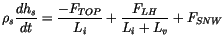 |
(6.3) |
where 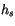 is the snow depth,
is the snow depth, 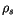 is the snow density,
is the snow density, 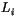 and
and
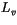 are the latent heats of fusion and vaporization, and
are the latent heats of fusion and vaporization, and  is the snowfall rate (see Table 6.1
for values of constants).
is the snowfall rate (see Table 6.1
for values of constants).
When CAM 3.0 is coupled to the mixed layer ocean and the sea ice is
snow-free, sea ice surface melt is computed from
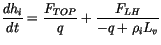 |
(6.4) |
where 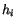 is the ice thickness,
is the ice thickness, 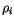 is the ice density, and
is the ice density, and
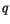 is the energy of melting of sea ice
(
is the energy of melting of sea ice
(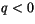 by definition,
see section 6.6 on brine pockets). Basal growth or melt is
computed from
by definition,
see section 6.6 on brine pockets). Basal growth or melt is
computed from
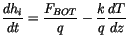 |
(6.5) |
where 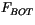 is the heat flux from the ocean to the ice (see
section 6.5). Finally an equation is needed to describe the
evolution of the ice concentration
is the heat flux from the ocean to the ice (see
section 6.5). Finally an equation is needed to describe the
evolution of the ice concentration 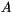 :
:
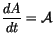 |
(6.6) |
where 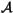 accounts for new ice formation over open water and
lateral melt (see section 6.7)
accounts for new ice formation over open water and
lateral melt (see section 6.7)
Parameterizations of albedo, surface fluxes, brine pockets, and
shortwave radiative transfer within the sea ice are given next.
Finally, the numerical solution to Eq. 6.1 is described.
Numerical methods for Eqs. 6.2 -6.6 are
straight-forward and hence are not described here.
Table 6.1:
List of Physical Constants
| Symbol |
Description |
Value |
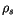 |
Density of snow |
330 kg m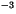 |
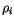 |
Density of ice |
917 kg m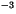 |
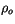 |
Density of surface ocean water |
1026 kg m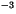 |
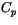 |
Specific heat of atmosphere dry |
1005 J kg K K |
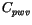 |
Specific heat of atmosphere water |
1810 J kg K K |
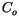 |
Specific heat of ocean water |
3996 J kg K K |
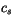 |
Specific heat of snow |
0 J kg K K |
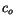 |
Specific heat of fresh ice |
2054 J kg K K |
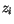 |
Aerodynamic roughness of ice |
5.0x10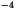 m m |
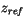 |
Reference height for bulk fluxes |
10 m |
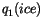 |
saturation specific humidity constant |
11637800 |
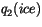 |
saturation specific humidity constant |
5897.8 |
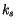 |
Thermal conductivity of snow |
0.31 W m K K |
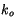 |
Thermal conductivity of fresh ice |
2.0340 W m K K |
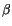 |
Thermal conductivity ice constant |
0.1172 W m ppt ppt |
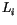 |
Latent heat of fusion of ice |
3.340x10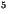 J kg J kg |
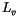 |
Latent heat of vaporization |
2.501x10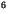 J kg J kg |
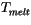 |
Melting temperature of top surface |
0 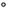 C C |
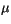 |
Ocean freezing temperature constant |
0.054 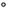 C ppt C ppt |
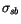 |
Stefan-Boltzmann constant |
5.67x10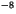 W m W m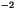 K K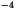 |
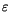 |
Ice emissivity |
0.95 |
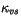 |
Ice SW visible extinction coefficient |
1.4 m |
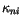 |
Ice SW near-ir extinction coefficient |
17.6 m |
NOTE: CSIM in CAM 3.0 uses the shared constants defined in Appendix
A.




Next: 6.3 Snow and Ice
Up: 6. Sea Ice Thermodynamics
Previous: 6.1 Basic assumptions
Contents
Jim McCaa
2004-06-22