



Next: 6.7 Open-Water Growth and
Up: 6. Sea Ice Thermodynamics
Previous: 6.5 Ice to Ocean
Contents
6.6 Brine Pockets and Internal Energy of Sea Ice
Shortwave radiative heating within the sea ice and conduction warms
the sea ice and opens brine pockets, melting the ice internally and
storing latent heat. This storage of latent heat is accounted for
explicitly by using a heat capacity and thermal conductivity that
depend on temperature and salinity following the work of Maykut and Untersteiner [125]
and Bitz and Lipscomb [20]. The equation for the heat capacity for sea ice 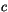 was first postulated by Untersteiner [176] and then later derived from
first principles by Ono [132]:
was first postulated by Untersteiner [176] and then later derived from
first principles by Ono [132]:
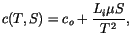 |
(6.40) |
where 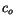 is the heat capacity for fresh ice,
is the heat capacity for fresh ice, 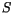 is the sea
ice salinity,
is the sea
ice salinity, 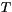 is the temperature, and
is the temperature, and 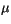 is an empirical
constant relating the freezing temperature of sea water linearly to
its salinity (
is an empirical
constant relating the freezing temperature of sea water linearly to
its salinity (
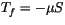 ).
).
Equation 6.40 can be multiplied by the sea ice density
and integrated to give the amount of energy 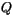 required to raise the
temperature of a unit volume of sea ice from
required to raise the
temperature of a unit volume of sea ice from 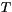 to
to 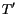 :
:
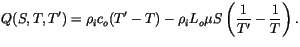 |
(6.41) |
If we take 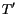 to be the melting temperature of ice with salinity
to be the melting temperature of ice with salinity 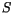 ,
then at
,
then at 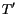 sea ice consists entirely of brine; that is,
the brine pockets have grown to encompass the entire mass of ice. The
amount of energy needed to melt a unit volume of sea ice of salinity
sea ice consists entirely of brine; that is,
the brine pockets have grown to encompass the entire mass of ice. The
amount of energy needed to melt a unit volume of sea ice of salinity
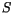 at temperature
at temperature 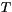 , resulting in meltwater at
, resulting in meltwater at 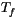 , is equal to
, is equal to
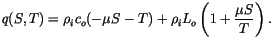 |
(6.42) |
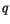 is referred to as the energy of melting of sea ice, and it
appears in Eqs. 6.4 and 6.5.
is referred to as the energy of melting of sea ice, and it
appears in Eqs. 6.4 and 6.5.
The thermal conductivity for sea ice  is
is
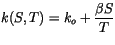 |
(6.43) |
where 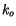 and
and 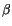 are empirical constants from Untersteiner [176].
are empirical constants from Untersteiner [176].
The vertical salinity profile is prescribed based on the work of
Maykut and Untersteiner [125] to be
![$\displaystyle S(w) = 1.6 \left[ 1 - \cos \left( \pi w^{\frac{0.407}{0.573 + w}} \right) \right]$](img3048.gif) |
(6.44) |
with the normalized coordinate 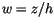 . This results in a profile
that varies from 0 ppt at ice surface increasing to
. This results in a profile
that varies from 0 ppt at ice surface increasing to 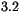 ppt at ice
base. Snow is assumed fresh.
ppt at ice
base. Snow is assumed fresh.
Shortwave radiative heating within the sea ice 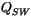 is equal to
the vertical gradient of the radiative transfer within the sea ice:
is equal to
the vertical gradient of the radiative transfer within the sea ice:
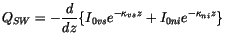 |
(6.45) |
where 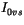 and
and 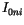 , the visible and near infrared radiation
fluxes that penetrate the surface, are reduced according to Beer's law
with the sea ice spectral extinction coefficients
, the visible and near infrared radiation
fluxes that penetrate the surface, are reduced according to Beer's law
with the sea ice spectral extinction coefficients
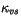 and
and
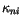 , respectively. For simplicity no shortwave radiation is
allowed to penetrate through snow and all of the near-infrared
radiation and 30% of the visible radiation is assumed to be absorbed
at the surface of sea ice (Gary Maykut, personal communication):
, respectively. For simplicity no shortwave radiation is
allowed to penetrate through snow and all of the near-infrared
radiation and 30% of the visible radiation is assumed to be absorbed
at the surface of sea ice (Gary Maykut, personal communication):
where 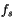 is the horizontal fraction of surface covered by snow
(see Eq. 6.11).
is the horizontal fraction of surface covered by snow
(see Eq. 6.11).




Next: 6.7 Open-Water Growth and
Up: 6. Sea Ice Thermodynamics
Previous: 6.5 Ice to Ocean
Contents
Jim McCaa
2004-06-22
![]() was first postulated by Untersteiner [176] and then later derived from
first principles by Ono [132]:
was first postulated by Untersteiner [176] and then later derived from
first principles by Ono [132]:
![]() required to raise the
temperature of a unit volume of sea ice from
required to raise the
temperature of a unit volume of sea ice from ![]() to
to ![]() :
:
![]() is
is
![]() is equal to
the vertical gradient of the radiative transfer within the sea ice:
is equal to
the vertical gradient of the radiative transfer within the sea ice: