The hybrid vertical coordinate that has been implemented in CAM 3.0 is
described in this section. The hybrid coordinate was developed by
Simmons and Strüfing [158] in order to provide a general framework for a
vertical coordinate which is terrain following at the Earth's surface,
but reduces to a pressure coordinate at some point above the
surface. The hybrid coordinate is more general in concept than the
modified ![]() scheme of Sangster [155], which is used in the
GFDL SKYHI model. However, the hybrid coordinate is normally specified
in such a way that the two coordinates are identical.
scheme of Sangster [155], which is used in the
GFDL SKYHI model. However, the hybrid coordinate is normally specified
in such a way that the two coordinates are identical.
The following description uses the same general development as Simmons and Strüfing [158], who based their development on the generalized vertical coordinate of Kasahara [84]. A specific form of the coordinate (the hybrid coordinate) is introduced at the latest possible point. The description here differs from Simmons and Strüfing [158] in allowing for an upper boundary at finite height (nonzero pressure), as in the original development by Kasahara. Such an upper boundary may be required when the equations are solved using vertical finite differences.
Deriving the primitive equations in a generalized terrain-following
vertical coordinate requires only that certain basic properties of the
coordinate be specified. If the surface pressure is ![]() , then we
require the generalized coordinate
, then we
require the generalized coordinate
![]() to satisfy:
to satisfy:
Given the above description of the coordinate, the continuous system
of equations can be written following Kasahara [84] and
Simmons and Strüfing [158]. The prognostic equations are:
In addition to the prognostic equations, three diagnostic equations are required:
Equations (3.1)-(3.16) are the complete set which must
be solved by a GCM. However, in order to solve them, the function
![]() must be specified. In advance of actually specifying
must be specified. In advance of actually specifying
![]() , the equations will be cast in a more convenient
form. Most of the changes to the equations involve simple applications
of the chain rule for derivatives, in order to obtain terms that will
be easy to evaluate using the predicted variables in the model. For
example, terms involving horizontal derivatives of
, the equations will be cast in a more convenient
form. Most of the changes to the equations involve simple applications
of the chain rule for derivatives, in order to obtain terms that will
be easy to evaluate using the predicted variables in the model. For
example, terms involving horizontal derivatives of ![]() must be
converted to terms involving only
must be
converted to terms involving only
![]() and
horizontal derivatives of
and
horizontal derivatives of ![]() . The former can be evaluated once the
function
. The former can be evaluated once the
function
![]() is specified.
is specified.
The vertical advection terms in (3.5), (3.6), (3.8), and (3.9) may be rewritten as:
The integrals which appear in (3.7), (3.15), and (3.16) can be written more conveniently by expanding the kernel as
The original primitive equations (3.3)-(3.7), together
with (3.8), (3.9), and (3.14)-(3.16)
can now be rewritten with the aid of (3.17), (3.18),
and (3.22).
In the actual definition of the hybrid coordinate, it is not necessary
to specify
![]() explicitly, since
(3.23)-(3.32) only requires that
explicitly, since
(3.23)-(3.32) only requires that ![]() and
and
![]() be determined. It is sufficient to specify
be determined. It is sufficient to specify
![]() and to let
and to let ![]() be defined implicitly. This will be
done in section 3.1.7. In the case that
be defined implicitly. This will be
done in section 3.1.7. In the case that
![]() and
and ![]() , (3.23)-(3.32)
can be reduced to the set of equations solved by CCM1.
, (3.23)-(3.32)
can be reduced to the set of equations solved by CCM1.
In practice, the solutions generated by solving the above equations
are excessively noisy. This problem appears to arise from aliasing
problems in the hydrostatic equation (3.30). The ![]() integral introduces a high order nonlinearity which enters directly
into the divergence equation (3.24). Large gravity waves are
generated in the vicinity of steep orography, such as in the Pacific
Ocean west of the Andes.
integral introduces a high order nonlinearity which enters directly
into the divergence equation (3.24). Large gravity waves are
generated in the vicinity of steep orography, such as in the Pacific
Ocean west of the Andes.
The noise problem is solved by converting the equations given above,
which use ![]() as a prognostic variable, to equations using
as a prognostic variable, to equations using
![]() . This results in the hydrostatic equation becoming
only quadratically nonlinear except for moisture contributions to
virtual temperature. Since the spectral transform method will be used
to solve the equations, gradients will be obtained during the
transform from wave to grid space. Outside of the prognostic equation
for
. This results in the hydrostatic equation becoming
only quadratically nonlinear except for moisture contributions to
virtual temperature. Since the spectral transform method will be used
to solve the equations, gradients will be obtained during the
transform from wave to grid space. Outside of the prognostic equation
for ![]() , all terms involving
, all terms involving ![]() will then appear as
will then appear as
![]() .
.
Equations (3.23)-(3.32) become:
The model described by (3.33)-(3.42), without the horizontal diffusion terms, together with boundary conditions (3.1) and (3.2), is integrated in time using the semi-implicit leapfrog scheme described below. The semi-implicit form of the time differencing will be applied to (3.34) and (3.36) without the horizontal diffusion sources, and to (3.37). In order to derive the semi-implicit form, one must linearize these equations about a reference state. Isolating the terms that will have their linear parts treated implicitly, the prognostic equations (3.33), (3.34), and (3.37) may be rewritten as:
In order to linearize (3.46)-(3.48), one specifies a reference state for temperature and pressure, then expands the equations about the reference state:
Expanding (3.46)-(3.48) about the reference state (3.49)-(3.51) and retaining only the linear terms explicitly, one obtains:
We will assume that centered differences are to be used for the
nonlinear terms, and the linear terms are to be treated implicitly by
averaging the previous and next time steps. Finite differences are
used in the vertical, and are described in the following sections. At
this stage only some very general properties of the finite difference
representation must be specified. A layering structure is assumed in
which field values are predicted on ![]() layer midpoints denoted by an
integer index,
layer midpoints denoted by an
integer index, ![]() (see Figure 3.1). The interface
between
(see Figure 3.1). The interface
between ![]() and
and
![]() is denoted by a half-integer index,
is denoted by a half-integer index,
![]() . The model top is at
. The model top is at
![]() , and the
Earth's surface is at
, and the
Earth's surface is at
![]() . It is further assumed that
vertical integrals may be written as a matrix (of order
. It is further assumed that
vertical integrals may be written as a matrix (of order ![]() ) times a
column vector representing the values of a field at the
) times a
column vector representing the values of a field at the ![]() grid
points in the vertical. The column vectors representing a vertical
column of grid points will be denoted by underbars, the matrices will
be denoted by bold-faced capital letters, and superscript
grid
points in the vertical. The column vectors representing a vertical
column of grid points will be denoted by underbars, the matrices will
be denoted by bold-faced capital letters, and superscript ![]() will
denote the vector transpose.
will
denote the vector transpose.
We shall impose a requirement on the vertical finite differences of
the model that they conserve the global integral of total energy
in the absence of sources and sinks. We need to derive
equations for kinetic and internal energy in order to impose this
constraint. The momentum equations (more painfully, the vorticity and
divergence equations) without the
![]() and
and
![]() contributions, can be combined with the continuity
equation
contributions, can be combined with the continuity
equation
The vertical integral of the second (vertical) transport term on the right-hand side of (3.60) should vanish. Since this term is obtained from the vertical advection terms for momentum, which will be finite differenced, we can construct a finite difference operator that will ensure that the vertical integral vanishes.
The vertical advection terms are the product of a vertical velocity
(
![]() ) and the vertical derivative of a
field (
) and the vertical derivative of a
field (
![]() ). The vertical velocity is defined in
terms of vertical integrals of fields (3.42), which are
naturally taken to interfaces. The vertical derivatives are also
naturally taken to interfaces, so the product is formed there, and
then adjacent interface values of the products are averaged to give a
midpoint value. It is the definition of the average that must be
correct in order to conserve kinetic energy under vertical advection
in (3.60). The derivation will be omitted here, the resulting
vertical advection terms are of the form:
). The vertical velocity is defined in
terms of vertical integrals of fields (3.42), which are
naturally taken to interfaces. The vertical derivatives are also
naturally taken to interfaces, so the product is formed there, and
then adjacent interface values of the products are averaged to give a
midpoint value. It is the definition of the average that must be
correct in order to conserve kinetic energy under vertical advection
in (3.60). The derivation will be omitted here, the resulting
vertical advection terms are of the form:
The last two terms in (3.60) contain the conversion between
kinetic and internal (potential) energy and the form drag. Neglecting
the transport terms, under assumption that global integrals will be
taken, noting that
![]() , and substituting for the geopotential
using (3.40), (3.60) can be written as:
, and substituting for the geopotential
using (3.40), (3.60) can be written as:
We now turn to the internal energy equation, obtained by combining the
thermodynamic equation (3.36), without the ![]() ,
, ![]() , and
, and
![]() terms, and the continuity equation (3.59):
terms, and the continuity equation (3.59):
The rate of change of total energy due to internal processes is
obtained by adding (3.65) and (3.67) and must
vanish. The first terms on the right-hand side of (3.65) and
(3.67) obviously cancel in the continuous form. When the
equations are discretized in the vertical, the terms will still
cancel, providing that the same definition is used for
![]() in the nonlinear terms of the
vorticity and divergence equations (3.38) and (3.39),
and in the
in the nonlinear terms of the
vorticity and divergence equations (3.38) and (3.39),
and in the ![]() term of (3.36) and (3.42).
term of (3.36) and (3.42).
The second terms on the right-hand side of (3.65) and (3.67) must also cancel in the global mean. This cancellation is enforced locally in the horizontal on the column integrals of (3.65) and (3.67), so that we require:
| (3.73) |
Given the definitions of vertical integrals in (3.70) and
(3.71) and of vertical advection in (3.61) and
(3.62) the model will conserve energy as long as we require
that
![]() and
and
![]() satisfy (3.75). We are,
of course, still neglecting lack of conservation due to the truncation
of the horizontal spherical harmonic expansions.
satisfy (3.75). We are,
of course, still neglecting lack of conservation due to the truncation
of the horizontal spherical harmonic expansions.
CAM 3.0 contains a horizontal diffusion term for ![]() , and
, and
![]() to prevent spectral blocking and to provide reasonable
kinetic energy spectra. The horizontal diffusion operator in CAM 3.0
is also used to ensure that the CFL condition is not violated in the
upper layers of the model. The horizontal diffusion is a linear
to prevent spectral blocking and to provide reasonable
kinetic energy spectra. The horizontal diffusion operator in CAM 3.0
is also used to ensure that the CFL condition is not violated in the
upper layers of the model. The horizontal diffusion is a linear
![]() form on
form on ![]() surfaces in the top three levels of the
model and a linear
surfaces in the top three levels of the
model and a linear ![]() form with a partial correction to
pressure surfaces for temperature elsewhere. The
form with a partial correction to
pressure surfaces for temperature elsewhere. The ![]() diffusion
near the model top is used as a simple sponge to absorb vertically
propagating planetary wave energy and also to control the strength of
the stratospheric winter jets. The
diffusion
near the model top is used as a simple sponge to absorb vertically
propagating planetary wave energy and also to control the strength of
the stratospheric winter jets. The ![]() diffusion coefficient
has a vertical variation which has been tuned to give reasonable
Northern and Southern Hemisphere polar night jets.
diffusion coefficient
has a vertical variation which has been tuned to give reasonable
Northern and Southern Hemisphere polar night jets.
In the top three model levels, the ![]() form of the horizontal
diffusion is given by
form of the horizontal
diffusion is given by
The horizontal diffusion operator is better applied to pressure
surfaces than to terrain-following surfaces (applying the operator on
isentropic surfaces would be still better). Although the governing
system of equations derived above is designed to reduce to pressure
surfaces above some level, problems can still occur from diffusion
along the lower surfaces. Partial correction to pressure surfaces of
harmonic horizontal diffusion (
![]() ) can be included using the relations:
) can be included using the relations:
The following finite-difference description details only the forecast
given by (3.87) and (3.90). The finite-difference
form of the forecast equation for water vapor will be presented later
in Section 3c. The general structure of the complete finite
difference equations is determined by the semi-implicit time
differencing and the energy conservation properties described above.
In order to complete the specification of the finite differencing, we
require a definition of the vertical coordinate. The actual
specification of the generalized vertical coordinate takes advantage
of the structure of the equations (3.33)-(3.42). The
equations can be finite-differenced in the vertical and, in time,
without having to know the value of ![]() anywhere. The quantities
that must be known are
anywhere. The quantities
that must be known are ![]() and
and
![]() at the grid
points. Therefore the coordinate is defined implicitly through the
relation:
at the grid
points. Therefore the coordinate is defined implicitly through the
relation:
The finite difference forms of the Dyn operator
(3.33)-(3.42), including semi-implicit time
integration are:
| (3.113) |
The spectral transform method is used in the horizontal exactly as in
CCM1. As shown earlier, the vertical and temporal aspects of the model
are represented by finite-difference approximations. The horizontal
aspects are treated by the spectral-transform method, which is
described in this section. Thus, at certain points in the
integration, the prognostic variables
![]() and
and ![]() are represented in terms of coefficients of a
truncated series of spherical harmonic functions, while at other
points they are given by grid-point values on a corresponding
Gaussian grid. In general, physical parameterizations and nonlinear
operations are carried out in grid-point space. Horizontal
derivatives and linear operations are performed in spectral space.
Externally, the model appears to the user to be a grid-point model,
as far as data required and produced by it. Similarly, since all
nonlinear parameterizations are developed and carried out in
grid-point space, the model also appears as a grid-point model for
the incorporation of physical parameterizations, and the user need not
be too concerned with the spectral aspects. For users interested in
diagnosing the balance of terms in the evolution equations, however,
the details are important and care must be taken to understand which
terms have been spectrally truncated and which have not. The algebra
involved in the spectral transformations has been presented in several
publications [24,46,118]. In this report,
we present only the details relevant to the model code; for more
details and general philosophy, the reader is referred to these
earlier papers.
are represented in terms of coefficients of a
truncated series of spherical harmonic functions, while at other
points they are given by grid-point values on a corresponding
Gaussian grid. In general, physical parameterizations and nonlinear
operations are carried out in grid-point space. Horizontal
derivatives and linear operations are performed in spectral space.
Externally, the model appears to the user to be a grid-point model,
as far as data required and produced by it. Similarly, since all
nonlinear parameterizations are developed and carried out in
grid-point space, the model also appears as a grid-point model for
the incorporation of physical parameterizations, and the user need not
be too concerned with the spectral aspects. For users interested in
diagnosing the balance of terms in the evolution equations, however,
the details are important and care must be taken to understand which
terms have been spectrally truncated and which have not. The algebra
involved in the spectral transformations has been presented in several
publications [24,46,118]. In this report,
we present only the details relevant to the model code; for more
details and general philosophy, the reader is referred to these
earlier papers.
The horizontal representation of an arbitrary variable ![]() consists
of a truncated series of spherical harmonic functions,
consists
of a truncated series of spherical harmonic functions,
The associated Legendre polynomials used in the model are normalized such that
The coefficients of the spectral representation (3.114) are given by
The Gaussian grid used for the north-south transformation is
generally chosen to allow un-aliased computations of quadratic terms
only. In this case, the number of Gaussian latitudes ![]() must satisfy
must satisfy
Although in the next section of this model description, we continue to
indicate the Gaussian quadrature as a sum from pole to pole, the code
actually deals with the symmetric and antisymmetric components of
variables and accumulates the sums from equator to pole only. The
model requires an even number of latitudes to easily use the symmetry
conditions. This may be slightly inefficient for some spectral
resolutions. We define a new index, which goes from ![]() at the point
next to the south pole to
at the point
next to the south pole to ![]() at the point next to the north pole and
not including 0 (there are no points at the equator or pole in the
Gaussian grid), i.e., let
at the point next to the north pole and
not including 0 (there are no points at the equator or pole in the
Gaussian grid), i.e., let ![]() and
and
![]() for
for
![]() and
and
![]() for
for
![]() ; then the summation
in (3.120) can be rewritten as
; then the summation
in (3.120) can be rewritten as
The model uses the spectral transform method [118] for
all nonlinear terms. However, the model can be thought of as starting
from grid-point values at time ![]() (consistent with the spectral
representation) and producing a forecast of the grid-point values at
time
(consistent with the spectral
representation) and producing a forecast of the grid-point values at
time
![]() (again, consistent with the spectral resolution).
The forecast procedure involves computation of the nonlinear terms
including physical parameterizations at grid points; transformation
via Gaussian quadrature of the nonlinear terms from grid-point space
to spectral space; computation of the spectral coefficients of the
prognostic variables at time
(again, consistent with the spectral resolution).
The forecast procedure involves computation of the nonlinear terms
including physical parameterizations at grid points; transformation
via Gaussian quadrature of the nonlinear terms from grid-point space
to spectral space; computation of the spectral coefficients of the
prognostic variables at time
![]() (with the implied spectral
truncation to the model resolution); and transformation back to
grid-point space. The details of the equations involved in the
various transformations are given in the next section.
(with the implied spectral
truncation to the model resolution); and transformation back to
grid-point space. The details of the equations involved in the
various transformations are given in the next section.
In order to describe the transformation to spectral space, for each equation we first group together all undifferentiated explicit terms, all explicit terms with longitudinal derivatives, and all explicit terms with meridional derivatives appearing in the Dyn operator. Thus, the vorticity equation (3.95) is rewritten
Formally, Equations (3.131)-(3.137) are transformed to
spectral space by performing the operations indicated in
(3.146) to each term. We see that the equations basically
contain three types of terms, for example, in the vorticity equation
the undifferentiated term
![]() , the longitudinally
differentiated term
, the longitudinally
differentiated term
![]() , and the
meridionally differentiated term
, and the
meridionally differentiated term
![]() . All
terms in the original equations were grouped into one of these terms
on the Gaussian grid so that they could be transformed at once.
. All
terms in the original equations were grouped into one of these terms
on the Gaussian grid so that they could be transformed at once.
Transformation of the undifferentiated term is obtained by straightforward application of (3.118)-(3.120),
| (3.147) | ||
| (3.148) | ||
| (3.149) |
The latitudinally differentiated term is handled by integration by parts using zero boundary conditions at the poles:
| (3.151) | ||
| (3.152) |
The prognostic equations can be converted to spectral form by summation over the Gaussian grid using (3.146), (3.150), and (3.154). The resulting equation for absolute vorticity is
The spectral form of the divergence equation (3.135) becomes
Equation (3.157) for vorticity is explicit and complete at this
point. However, the remaining equations
(3.159)-(3.163) are coupled. They are solved by
eliminating all variables except
![]() :
:
As mentioned earlier, the horizontal diffusion in (3.88) and
(3.91) is computed implicitly via time splitting after the
transformations into spectral space and solution of the semi-implicit
equations. In the following, the ![]() and
and ![]() equations have a
similar form, so we write only the
equations have a
similar form, so we write only the ![]() equation:
equation:
The extra term is present in (3.167), (3.171) and (3.173) to prevent damping of uniform rotations. The solutions are just
The diffusion of ![]() is not complete at this stage. In order to make
the partial correction from
is not complete at this stage. In order to make
the partial correction from ![]() to
to ![]() in (3.82) local, it
is not included until grid-point values are available. This requires
that
in (3.82) local, it
is not included until grid-point values are available. This requires
that
![]() also be transformed from spectral to grid-point
space. The values of the coefficients
also be transformed from spectral to grid-point
space. The values of the coefficients ![]() and
and ![]() for the
standard T42 resolution are
for the
standard T42 resolution are
![]() m
m![]() sec
sec![]() and
and
![]() m
m![]() sec
sec![]() , respectively.
, respectively.
Occasionally, with poorly balanced initial conditions, the model
exhibits numerical instability during the beginning of an integration
because of excessive noise in
the solution. Therefore, an optional divergence damping is included
in the model to be applied over the first few days. The damping has
an initial e-folding time of ![]() and linearly decreases to 0
over a specified number of days,
and linearly decreases to 0
over a specified number of days, ![]() , usually set to be
2. The damping is computed implicitly via time splitting after
the horizontal diffusion.
, usually set to be
2. The damping is computed implicitly via time splitting after
the horizontal diffusion.
After the prognostic variables are completed at time ![]() in spectral
space
in spectral
space
![]() ,
,
![]() ,
,
![]() ,
,
![]() they
are transformed to grid space. For a variable
they
are transformed to grid space. For a variable ![]() , the
transformation is given by
, the
transformation is given by
The horizontal diffusion tendencies are also transformed back to grid space. The spectral coefficients for the horizontal diffusion tendencies follow from (3.167) and (3.168):
After grid-point values are calculated, frictional heating rates are
determined from the momentum diffusion tendencies and are added to the
temperature, and the partial correction of the ![]() diffusion
from
diffusion
from ![]() to
to ![]() surfaces is applied to
surfaces is applied to ![]() . The frictional heating
rate is calculated from the kinetic energy tendency produced by the
momentum diffusion
. The frictional heating
rate is calculated from the kinetic energy tendency produced by the
momentum diffusion
| (3.194) | ||
| (3.195) | ||
| (3.196) |
The corrections are added to the diffusion tendencies calculated earlier (3.188) to give the total temperature tendency for diagnostic purposes:
The forecast equation for water vapor specific humidity and
constituent mixing ratio in the ![]() system is from (3.36)
excluding sources and sinks.
system is from (3.36)
excluding sources and sinks.
The parameterizations are time-split in the moisture equation. The
tendency sources have already been added to the time level
![]() . The semi-Lagrangian advection step is subdivided into
horizontal and vertical advection sub-steps, which, in an Eulerian
form, would be written
. The semi-Lagrangian advection step is subdivided into
horizontal and vertical advection sub-steps, which, in an Eulerian
form, would be written
The horizontal departure points are found by first iterating for the
mid-point of the trajectory, using winds at time ![]() , and a first
guess as the location of the mid-point of the previous time step
, and a first
guess as the location of the mid-point of the previous time step
Once the iteration of (3.204) and (3.205) is complete, the departure point is given by
The form given by (3.204)-(3.207) is inaccurate near the
poles and thus is only used for arrival points equatorward of
70![]() latitude. Poleward of 70
latitude. Poleward of 70![]() we transform to a local
geodesic coordinate for the calculation at each arrival point. The
local geodesic coordinate is essentially a rotated spherical
coordinate system whose equator goes through the arrival point.
Details are provided in Williamson and Rasch [186]. The transformed system
is rotated about the axis through
we transform to a local
geodesic coordinate for the calculation at each arrival point. The
local geodesic coordinate is essentially a rotated spherical
coordinate system whose equator goes through the arrival point.
Details are provided in Williamson and Rasch [186]. The transformed system
is rotated about the axis through
![]() and
and
![]() , by an
angle
, by an
angle ![]() so the equator goes through
so the equator goes through
![]() . The longitude of the transformed system is chosen
to be zero at the arrival point. If the local geodesic system is
denoted by
. The longitude of the transformed system is chosen
to be zero at the arrival point. If the local geodesic system is
denoted by
![]() , with
velocities
, with
velocities
![]() , the two systems are
related by
, the two systems are
related by
The interpolants are most easily defined on the interval 0
![]() . Define
. Define
Following (3.2.12) and (3.2.13) of Hildebrand [71], the Lagrangian cubic polynomial interpolant used for the velocity interpolation, is given by
The derivative approximations used in (3.214) for ![]() are
obtained by differentiating (3.215) with respect to
are
obtained by differentiating (3.215) with respect to ![]() ,
replacing
,
replacing ![]() by
by ![]() and evaluating the result at
and evaluating the result at ![]() equal
equal ![]() and
and ![]() . With these derivative estimates, the Hermite cubic
interpolant (3.214) is equivalent to the Lagrangian
(3.215). If we denote the four point stencil
. With these derivative estimates, the Hermite cubic
interpolant (3.214) is equivalent to the Lagrangian
(3.215). If we denote the four point stencil
![]() by
by
![]() the cubic derivative estimates are
the cubic derivative estimates are
The two dimensional
![]() interpolant is
obtained as a tensor product application of the one-dimensional
interpolants, with
interpolant is
obtained as a tensor product application of the one-dimensional
interpolants, with ![]() interpolations done first. Assume the
departure point falls in the grid box
interpolations done first. Assume the
departure point falls in the grid box
![]() and
and
![]() . Four
. Four ![]() interpolations are
performed to find
interpolations are
performed to find ![]() values at
values at
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . This is followed by one interpolation in
. This is followed by one interpolation in ![]() using these four values to obtain the value at
using these four values to obtain the value at
![]() . Cyclic continuity is used in longitude. In latitude,
the grid is extended to include a pole point (row) and one row across
the pole. The pole row is set equal to the average of the row next to
the pole for
. Cyclic continuity is used in longitude. In latitude,
the grid is extended to include a pole point (row) and one row across
the pole. The pole row is set equal to the average of the row next to
the pole for ![]() and to wavenumber 1 components for
and to wavenumber 1 components for ![]() and
and ![]() . The
row across the pole is filled with the values from the first row below
the pole shifted
. The
row across the pole is filled with the values from the first row below
the pole shifted ![]() in longitude for
in longitude for ![]() and minus the value
shifted by
and minus the value
shifted by ![]() in longitude for
in longitude for ![]() and
and ![]() .
.
Once the departure point is known, the constituent value of
![]() is obtained as indicated in (3.202) by Hermite cubic
interpolation (3.214), with cubic derivative estimates
(3.215) and (3.216) modified to satisfy the Sufficient
Condition for Monotonicity with C
is obtained as indicated in (3.202) by Hermite cubic
interpolation (3.214), with cubic derivative estimates
(3.215) and (3.216) modified to satisfy the Sufficient
Condition for Monotonicity with C![]() continuity (SCMO) described
below. Define
continuity (SCMO) described
below. Define
![]() by
by
The horizontal semi-Lagrangian sub-step (3.202) is followed by
the vertical step (3.203). The vertical velocity ![]() is
obtained from that diagnosed in the dynamical calculations
(3.94) by
is
obtained from that diagnosed in the dynamical calculations
(3.94) by
This section describes original and modified fixers used for the Eulerian and semi-Lagrangian dynamical cores.
Let ![]() ,
,
![]() and
and ![]() denote the values of air mass,
pressure intervals, and water vapor specific humidity at the
beginning of the time step (which are the same as the values
at the end of the previous time step.)
denote the values of air mass,
pressure intervals, and water vapor specific humidity at the
beginning of the time step (which are the same as the values
at the end of the previous time step.)
![]() ,
,
![]() and
and ![]() are the values after fixers are applied
at the end of the time step.
are the values after fixers are applied
at the end of the time step.
![]() ,
,
![]() and
and ![]() are the values after the parameterizations
have updated the moisture field and tracers.
are the values after the parameterizations
have updated the moisture field and tracers.
Since the physics parameterizations do not change the surface pressure,
![]() and
and
![]() are also the values at the beginning
of the time step.
are also the values at the beginning
of the time step.
The fixers which ensure conservation are applied to the dry
atmospheric mass, water vapor specific humidity and constituent mixing
ratios. For water vapor and atmospheric mass the desired discrete
relations, following Williamson and Olson [185] are
We note that there is a small error in (3.241). Consider
a situation in which moisture is transported by a physical
parameterization, but there is no source or sink of moisture. Under
this circumstance
![]() , but the surface pressure is not
allowed to change. Since
, but the surface pressure is not
allowed to change. Since
![]() , there is an implied change of dry mass of dry air
in the layer, and even in circumstances where there is no change
of dry mixing ratio
, there is an implied change of dry mass of dry air
in the layer, and even in circumstances where there is no change
of dry mixing ratio ![]() there would be an implied change in mass of the tracer. The
solution to this inconsistency is to define a dry air mass only
once within the model time step, and use it consistently throughout
the model. In this revision, we have chosen to fix the dry air mass in
the model
time step where the surface pressure is updated, e.g. at the end of
the model time step. Therefore, we now replace (3.241) with
there would be an implied change in mass of the tracer. The
solution to this inconsistency is to define a dry air mass only
once within the model time step, and use it consistently throughout
the model. In this revision, we have chosen to fix the dry air mass in
the model
time step where the surface pressure is updated, e.g. at the end of
the model time step. Therefore, we now replace (3.241) with
There is a corresponding change in the first term of the numerator of
(3.243) in which ![]() is replace by
is replace by ![]() . CAM 3.0uses
(3.243) for water substances and constituents affecting the
temperature field to prevent changes to the IPCC simulations. In the
future, constituent fields may use a corrected version of
(3.243).
. CAM 3.0uses
(3.243) for water substances and constituents affecting the
temperature field to prevent changes to the IPCC simulations. In the
future, constituent fields may use a corrected version of
(3.243).
![$\displaystyle \int\limits_3 {1 \over g} \left[ c_p T^+ + \Phi_s + {1 \over 2} \left( {u^+}^2 + {v^+}^2 \right) \right] \Delta p^+ = {\boldsymbol {E}}$](img692.gif) |
(3.246) | |
![$\displaystyle \int\limits_3 {1 \over g} \left[ c_p T^- + \Phi_s + {1 \over 2} \left( {u^-}^2 + {v^-}^2 \right) \right] \Delta p^- + {\boldsymbol {S}}$](img694.gif) |
(3.247) |
![$\displaystyle {\boldsymbol {S}} = \int\limits_2 \left[ \left( FSNT - FLNT \right) - \left( FSNS - FLNS - SHFLX - \rho_{H_2O} L_v PRECT \right) - \right] \Delta t$](img695.gif) |
(3.248) |
| (3.249) |
| (3.250) |
| (3.251) | |||
| (3.252) | |||
| (3.253) |
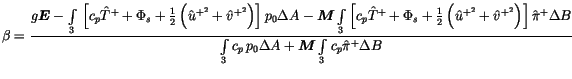 |
(3.254) |
| global rms |
![$\displaystyle = \left[ \int_3 (\zeta^n + f)^2 dV \right]^{1/2} ,$](img721.gif) |
(3.258) |
| global rms |
![$\displaystyle = \left [\int_3 (\delta^n)^2 dV \right]^{1/2} ,$](img723.gif) |
(3.259) |
| global rms |
![$\displaystyle = \left[ \int_3 (T^r + T'^n)^2 dV \right]^{1/2} ,$](img725.gif) |
(3.260) |
| global average mass times |
(3.261) | |
| global average mass of moisture |
(3.262) |