The two-time-level semi-implicit semi-Lagrangian spectral transform
dynamical core in CAM 3.0 evolved from the three-time-level CCM2
semi-Lagrangian version detailed in Williamson and Olson [185] hereafter
referred to as W&O94. As a first approximation, to convert from a
three-time-level scheme to a two-time-level scheme, the time level
index n-1 becomes n, the time level index n becomes n+
![]() ,
and
,
and ![]() becomes
becomes ![]() . Terms needed at n+
. Terms needed at n+
![]() are extrapolated in time using time n and n-1 terms, except the
Coriolis term which is implicit as the average of time n and n+1. This
leads to a more complex semi-implicit equation to solve. Additional
changes have been made in the scheme to incorporate advances in
semi-Lagrangian methods developed since W&O94. In the following,
reference is made to changes from the scheme developed in W&O94. The
reader is referred to that paper for additional details of the
derivation of basic aspects of the semi-Lagrangian
approximations. Only the details of the two-time-level approximations
are provided here.
are extrapolated in time using time n and n-1 terms, except the
Coriolis term which is implicit as the average of time n and n+1. This
leads to a more complex semi-implicit equation to solve. Additional
changes have been made in the scheme to incorporate advances in
semi-Lagrangian methods developed since W&O94. In the following,
reference is made to changes from the scheme developed in W&O94. The
reader is referred to that paper for additional details of the
derivation of basic aspects of the semi-Lagrangian
approximations. Only the details of the two-time-level approximations
are provided here.
The semi-Lagrangian dynamical core adopts the same hybrid vertical
coordinate (![]() ) as the Eulerian core defined by
) as the Eulerian core defined by
In the ![]() system the hydrostatic equation is approximated in a
general way by
system the hydrostatic equation is approximated in a
general way by
The semi-implicit equations are linearized about a reference state
with constant ![]() and
and ![]() . We choose
. We choose
| (3.265) |
To ameliorate the mountain resonance problem,
Ritchie and Tanguay [148] introduce a perturbation
![]() surface pressure prognostic variable
surface pressure prognostic variable
| (3.266) | |||
| (3.267) |
Variables needed at time (
![]() ) are obtained by
extrapolation
) are obtained by
extrapolation
| (3.268) |
Lagrangian polynomial quasi-cubic interpolation is used in the prognostic equations for the dynamical core. Monotonic Hermite quasi-cubic interpolation is used for tracers. Details are provided in the Eulerian Dynamical Core description. The trajectory calculation uses tri-linear interpolation of the wind field.
The discrete semi-Lagrangian, semi-implicit continuity equation is
obtained from (16) of W&O94 modified to be spatially uncentered by a
fraction ![]() , and to predict
, and to predict
![]()
![$\displaystyle \left\{ \left({\rm ln} p_{s{_{l}}}'\right)^{n+1}_{_{A}} - \left[...
...)^{n} + { \Phi_s \over RT^r } \right] _{D_{2}} \right\} \Bigg/ \Delta t =$](img755.gif) |
||
![$\displaystyle - {1\over 2} \bigg\lbrace \left[ \left(1 + \epsilon \right) \Delt...
...dot\eta {\partial p \over \partial\eta}\right)_l\right]^{n}_{D_{2}}\bigg\rbrace$](img756.gif) |
(3.269) | |
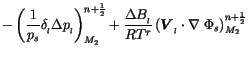 |
||
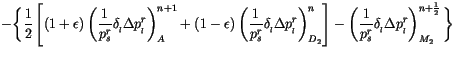 |
| (3.270) | ||
|
and
| ||
| (3.271) | ||
The surface pressure forecast equation is obtained by summing over all
levels and is related to (18) of W&O94 but is spatially uncentered
and uses
![]()
![$\displaystyle \sum^K_{l=1} \Delta
B_l
\left[ \left({\rm ln} p_{s{_{l}}} \right...
...\over p_s}
\dot\eta {\partial p \over
\partial\eta}\right)_l\right]^{n}_{D_{2}}$](img768.gif) |
|||
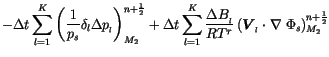 |
(3.272) | ||
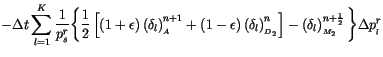 |
The corresponding
![]() equation for the semi-implicit development
follows and is related to
(19) of W&O94, again spatially uncentered and using
equation for the semi-implicit development
follows and is related to
(19) of W&O94, again spatially uncentered and using
![]() .
.
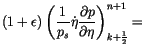 |
![$\displaystyle - {2 \over \Delta t} \bigg\lbrace B_{k+ {1\over 2}} \left({\rm ln...
...m ln}\; p_{s_l} \right)^{n} + { \Phi_s \over RT^r } \right] _{D_2} \bigg\rbrace$](img774.gif) |
|
![$\displaystyle - \sum^k_{l=1}\left[ \left(1 - \epsilon \right)\Delta \left({1 \over p_s} \dot\eta {\partial p \over \partial\eta}\right)_l \right]^{n}_{D_{2}}$](img775.gif) |
(3.273) | |
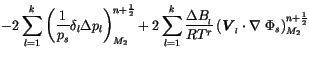 |
||
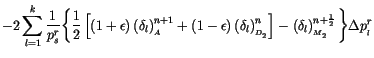 |
This is not the actual equation used to determine
![]() in the code. The
equation actually used in the code to calculate
in the code. The
equation actually used in the code to calculate
![]() involves only the
divergence at time (
involves only the
divergence at time (![]() ) with
) with
![]() eliminated.
eliminated.
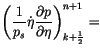 |
||
![$\displaystyle \left[ \sum^k_{l=1} - B_{k+{1\over 2}}\sum^K_{l=1}\right] \Delt...
...ft[ \left({\rm ln}\; p_{s_l} \right)^{n} + { \Phi_s \over RT^r } \right] _{D_2}$](img782.gif) |
||
![$\displaystyle \left[ \sum^k_{l=1} - B_{k+{1\over 2}}\sum^K_{l=1}\right] \left...
... \over p_s} \dot\eta {\partial p \over \partial \eta}\right)_l\right]^{n}_{D_2}$](img784.gif) |
||
![$\displaystyle \left[ \sum^k_{l=1} - B_{k+{1\over 2}}\sum^K_{l=1}\right] \left({1 \over p_s} \delta_l \Delta p_l \right)^{n+{1\over 2}}_{M_2}$](img786.gif) |
(3.274) | |
![$\displaystyle \left[ \sum^k_{l=1} - B_{k+{1\over 2}}\sum^K_{l=1}\right] {\Del...
...ft( {\boldsymbol {V}}_{_{l}} \cdot \nabla \;\Phi_s \right)^{n+{1\over 2}}_{M_2}$](img788.gif) |
||
![$\displaystyle \left[ \sum^k_{l=1} - B_{k+{1\over 2}}\sum^K_{l=1}\right] {1 \o...
...ght] - \left(\delta_l \right)^{n+{1\over 2}}_{_{M_2}} \bigg\rbrace \Delta p^r_l$](img789.gif) |
The thermodynamic equation is obtained from (25) of W&O94 modified to
be spatially uncentered and to use
![]() . In addition
Hortal's modification [172] is included, in which
. In addition
Hortal's modification [172] is included, in which
![$\displaystyle {d \over dt} \left[ -\left(p_s B {\partial T \over \partial p}\right)_{ref} { \Phi_s \over RT^r } \right]$](img791.gif) |
(3.275) |
![$\displaystyle \left\{ \left\{\left[
-\left(p_s B(\eta) {\partial T \over \parti...
...ght)_{ref}
{ \Phi_s \over RT^r } \right]_D^{n} \right\} \Bigg/ \Delta t \right.$](img796.gif) |
|||
![$\displaystyle \left. +{ 1 \over RT^r }\left[
\left(p_s B(\eta) {\partial T \ove...
...a)
{\partial T \over \partial p}\right)_{ref} \right]_M^{n+{1\over 2}}
\right\}$](img797.gif) |
|||
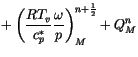 |
|||
![$\displaystyle + {RT^r \over c_p} {p_s^r \over p^r}\left[ B(\eta)
{d_2\;{\rm ln}...
...eft({1 \over p_s}
\dot \eta {\partial p \over \partial \eta} \right)}^t \right]$](img799.gif) |
(3.276) | ||
![$\displaystyle - {RT^r \over c_p} {p_s^r \over p^r} \left[\left({p \over
p_s}\right) \left( {\omega \over p} \right) \right]^{n+{1\over
2}}_M$](img800.gif) |
|||
![$\displaystyle - {RT^r \over c_p} {p_s^r \over p^r} B(\eta) \left[ {1
\over RT^r} {\boldsymbol {V}} \cdot \nabla \;\Phi_s
\right]^{n+{1\over 2}}_{M_2}$](img801.gif) |
The calculation of
![]() follows that of the ECMWF (Research Manual 3, ECMWF
Forecast Model, Adiabatic Part, ECMWF Research Department, 2nd
edition, 1/88, pp 2.25-2.26) Consider a constant lapse rate atmosphere
follows that of the ECMWF (Research Manual 3, ECMWF
Forecast Model, Adiabatic Part, ECMWF Research Department, 2nd
edition, 1/88, pp 2.25-2.26) Consider a constant lapse rate atmosphere
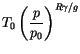 |
(3.277) | ||
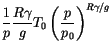 |
(3.278) | ||
| (3.279) | |||
| (3.280) | |||
| (3.281) | |||
| (3.282) | |||
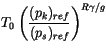 |
(3.283) | ||
| (3.284) | |||
| (3.285) | |||
| (3.286) | |||
| (3.287) | |||
| (3.288) |
The momentum equations follow from (3) of W&O94 modified to be
spatially uncentered, to use
![]() , and with the Coriolis
term implicit following Côté and Staniforth [43] and
Temperton [171]. The semi-implicit, semi-Lagrangian momentum
equation at level
, and with the Coriolis
term implicit following Côté and Staniforth [43] and
Temperton [171]. The semi-implicit, semi-Lagrangian momentum
equation at level ![]() (but with the level subscript
(but with the level subscript ![]() suppressed) is
suppressed) is
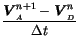 |
|||
![$\displaystyle -{1 \over 2}\bigg\lbrace \left(1 + \epsilon
\right)
\left[ \nab...
...ght)
+ RT_v {B \over p} p_s \nabla {\rm ln} p_s
\right]^{n+{1\over 2}}_{_{A}}$](img827.gif) |
|||
![$\displaystyle \phantom{-{1 \over 2}} + \left(1 - \epsilon
\right)
\left[ \nabla...
...{B \over p} p_s \nabla {\rm ln} p_s
\right]^{n+{1\over 2}}_{_{D}}\bigg\rbrace$](img828.gif) |
|||
| (3.289) | |||
The gradient of the geopotential is more complex than in the ![]() system because the hydrostatic matrix
system because the hydrostatic matrix
![]() depends on the
local pressure:
depends on the
local pressure:
| (3.290) |
| (3.291) |
| (3.292) |
| (3.293) |
The momentum equation can be written as
By combining terms, 3.294 can be written in general as
| (3.296) | |||
| (3.297) |
W&O94 followed Bates et al. [13] which ignored rotating the vector
to remain parallel to the earth's surface during translation. We
include that factor by keeping the length of the vector written in
terms of
![]() the same as the length of the vector written in terms of
the same as the length of the vector written in terms of
![]() .
Thus, (10) of W&O94 becomes
.
Thus, (10) of W&O94 becomes
| (3.298) |
![$\displaystyle \gamma = \left[ { {\cal U}_{_{D}}^2 + {\cal V}_{_{D}}^2 \over \le...
...}}\beta^u_{_{A}} + {\cal V}_{_{D}}\beta^v_{_{A}}\right)^2 } \right]^{1 \over 2}$](img868.gif) |
(3.299) |
| (3.300) |
| (3.301) |
| (3.302) | |||
| (3.303) |
| (3.304) | |||
| (3.305) |
| (3.306) | |||
| (3.307) |
Transform to spectral space as described in the description of the
Eulerian spectral transform dynamical core. Note, from (4.5b) and
(4.6) on page 177 of Machenhauer [118]
| (3.308) | |||
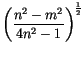 |
(3.309) |
| (3.310) |
| (3.311) | |||
| (3.312) | |||
| (3.313) | |||
| (3.314) |
| (3.315) | |||
| (3.316) |
| (3.317) | ||
|
and
| ||
| (3.318) | ||
| (3.319) | ||
| (3.320) | ||
| (3.321) | |||
| (3.322) |
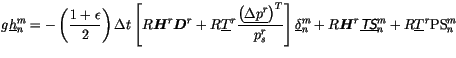 |
(3.323) |
Define
![]() and
and
![]() so
that
so
that
| (3.324) |
| (3.325) |
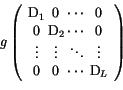 |
(3.326) | ||
| (3.327) | |||
| (3.328) |
| (3.329) | ||||
| (3.330) | ||||
| (3.331) |
| (3.332) | |||
| (3.333) | |||
| (3.334) | |||
| (3.335) |
For each vertical mode, i.e. element of
![]() , and for each Fourier wavenumber
, and for each Fourier wavenumber ![]() we
have a system of equations in
we
have a system of equations in ![]() to solve. In following we drop the
Fourier index
to solve. In following we drop the
Fourier index ![]() and the modal element index
and the modal element index ![]() from the
notation.
from the
notation.
| (3.336) | |||
| (3.337) | |||
| (3.338) |
Substitute
![]() and
and
![]() into the
into the
![]() equation.
equation.
![$\displaystyle \left[ {\cal A}_n + \left( {1 + \epsilon \over 2}\right)^2 \left(...
...cal B}^-}_{n+1} + {{\cal B}^-}_n {\cal A}_{n-1}^{-1} {{\cal B}^+}_{n-1} \right]$](img966.gif) |
(3.339) | ||
At the end of the system, the boundary conditions are
| (3.340) | ||||
| (3.341) |
For each ![]() and
and ![]() we have the general systems of equations
we have the general systems of equations
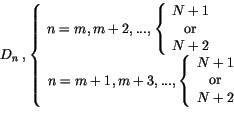 |
(3.342) | ||
| 0 | (3.343) | ||
| 0 | (3.344) |
Assume solutions of the form
| (3.345) |
| (3.346) | |||
| (3.347) |
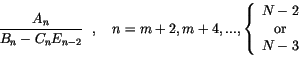 |
(3.348) | ||
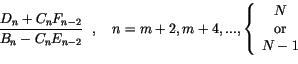 |
(3.349) |
| (3.350) |
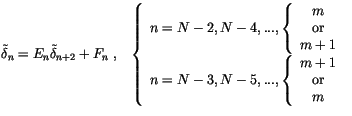 |
(3.351) |
Divergence in physical space is obtained from the vertical mode coefficients by
| (3.352) |
| (3.353) | |||
| (3.354) | |||
| (3.355) |
The trajectory calculation follows Hortal [77] Let
![]() denote the position vector of the parcel,
denote the position vector of the parcel,
| (3.356) |
| (3.357) |
| (3.358) |
| (3.359) |
| (3.360) | ||
|
giving
| ||
| (3.361) | ||