



Next: 4.2 Shallow/Middle Tropospheric Moist
Up: 4. Model Physics
Previous: 4. Model Physics
Contents
Subsections
4.1 Deep Convection
The process of deep convection is treated with a parameterization
scheme developed by Zhang and McFarlane [199]. The scheme is based on a plume
ensemble approach where it is assumed that an ensemble of convective
scale updrafts (and the associated saturated downdrafts) may exist
whenever the atmosphere is conditionally unstable in the lower
troposphere. The updraft ensemble is comprised of plumes sufficiently
buoyant so as to penetrate the unstable layer, where all plumes have
the same upward mass flux at the bottom of the convective layer.
Moist convection occurs only when there is convective available
potential energy (CAPE) for which parcel ascent from the sub-cloud
layer acts to destroy the CAPE at an exponential rate using a
specified adjustment time scale. For the convenience of the reader we
will review some aspects of the formulation, but refer the interested
reader to Zhang and McFarlane [199] for additional detail, including behavioral
characteristics of the parameterization scheme. Evaporation of
convective precipitation is computed following the procedure described
in section 4.3.
The large-scale budget equations distinguish between a cloud and
sub-cloud layer where temperature and moisture response to convection
in the cloud layer is written in terms of bulk convective fluxes as
for 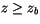 , where
, where 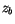 is the height of the cloud base. For
is the height of the cloud base. For
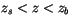 , where
, where 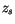 is the surface height, the sub-cloud layer
response is written as
is the surface height, the sub-cloud layer
response is written as
where the net vertical mass flux in the convective region, 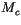 , is
comprised of upward,
, is
comprised of upward, 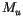 , and downward,
, and downward, 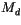 , components,
, components, 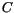 and
and
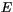 are the large-scale condensation and evaporation rates,
are the large-scale condensation and evaporation rates, 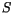 ,
,
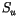 ,
, 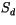 ,
, 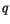 ,
, 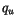 ,
, 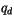 , are the corresponding values of the
dry static energy and specific humidity, and
, are the corresponding values of the
dry static energy and specific humidity, and 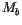 is the cloud base
mass flux.
is the cloud base
mass flux.
The updraft ensemble is represented as a collection of entraining
plumes, each with a characteristic fractional entrainment rate
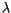 . The moist static energy in each plume
. The moist static energy in each plume 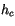 is given by
is given by
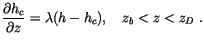 |
(4.6) |
Mass carried upward by the plumes is detrained into the environment in
a thin layer at the top of the plume, 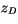 , where the detrained air
is assumed to have the same thermal properties as in the environment
(
, where the detrained air
is assumed to have the same thermal properties as in the environment
(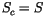 ). Plumes with smaller
). Plumes with smaller 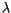 penetrate to larger
penetrate to larger
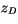 . The entrainment rate
. The entrainment rate 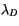 for the plume which detrains
at height
for the plume which detrains
at height 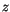 is then determined by solving (4.6), with lower
boundary condition
is then determined by solving (4.6), with lower
boundary condition
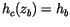 :
:
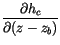 |
 |
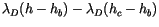 |
(4.7) |
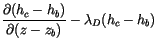 |
 |
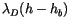 |
(4.8) |
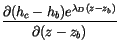 |
 |
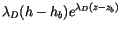 |
(4.9) |
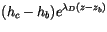 |
 |
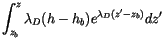 |
(4.10) |
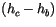 |
 |
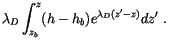 |
(4.11) |
Since the plume is saturated, the detraining air must have
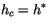 , so that
, so that
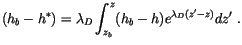 |
(4.12) |
Then, 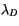 is determined by solving (4.12) iteratively
at each
is determined by solving (4.12) iteratively
at each 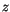 .
.
The top of the shallowest of the convective plumes, 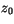 is assumed
to be no lower than the mid-tropospheric minimum in saturated moist
static energy,
is assumed
to be no lower than the mid-tropospheric minimum in saturated moist
static energy, 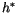 , ensuring that the cloud top detrainment is
confined to the conditionally stable portion of the atmospheric
column. All condensation is assumed to occur within the updraft
plumes, so that
, ensuring that the cloud top detrainment is
confined to the conditionally stable portion of the atmospheric
column. All condensation is assumed to occur within the updraft
plumes, so that 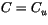 . Each plume is assumed to have the same
value for the cloud base mass flux
. Each plume is assumed to have the same
value for the cloud base mass flux 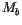 , which is specified
below. The vertical distribution of the cloud updraft mass flux is
given by
, which is specified
below. The vertical distribution of the cloud updraft mass flux is
given by
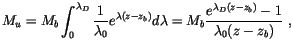 |
(4.13) |
where 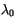 is the maximum detrainment rate, which occurs for
the plume detraining at height
is the maximum detrainment rate, which occurs for
the plume detraining at height 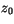 , and
, and 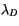 is the
entrainment rate for the updraft that detrains at height
is the
entrainment rate for the updraft that detrains at height 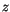 .
Detrainment is confined to regions where
.
Detrainment is confined to regions where 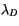 decreases with
height, so that the total detrainment
decreases with
height, so that the total detrainment 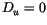 for
for 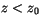 . Above
. Above
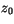 ,
,
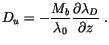 |
(4.14) |
The total entrainment rate is then just given by the change in mass
flux and the total detrainment,
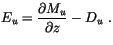 |
(4.15) |
The updraft budget equations for dry static energy, water vapor mixing
ratio, moist static energy, and cloud liquid water, 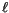 , are:
, are:
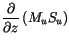 |
 |
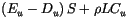 |
(4.16) |
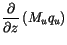 |
 |
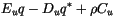 |
(4.17) |
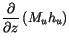 |
 |
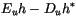 |
(4.18) |
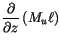 |
 |
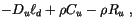 |
(4.19) |
where (4.18) is formed from (4.16) and (4.17)
and detraining air has been assumed to be saturated (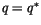 and
and
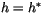 ). It is also assumed that the liquid content of the detrained
air is the same as the ensemble mean cloud water (
). It is also assumed that the liquid content of the detrained
air is the same as the ensemble mean cloud water (
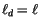 ).
The conversion from cloud water to rain water is given by
).
The conversion from cloud water to rain water is given by
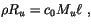 |
(4.20) |
following Lord et al. [116], with
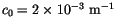 .
.
Since 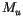 ,
, 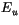 and
and 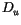 are given by (4.13-4.15),
and
are given by (4.13-4.15),
and 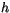 and
and 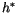 are environmental profiles, (4.18) can be
solved for
are environmental profiles, (4.18) can be
solved for 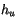 , given a lower boundary condition. The lower boundary
condition is obtained by adding a
, given a lower boundary condition. The lower boundary
condition is obtained by adding a 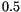 K temperature perturbation to
the dry (and moist) static energy at cloud base, or
K temperature perturbation to
the dry (and moist) static energy at cloud base, or
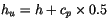 at
at 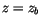 . Below the lifting condensation level (LCL),
. Below the lifting condensation level (LCL),
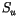 and
and 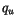 are given by (4.16) and (4.17). Above
the LCL,
are given by (4.16) and (4.17). Above
the LCL, 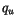 is reduced by condensation and
is reduced by condensation and 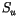 is increased by
the latent heat of vaporization. In order to obtain to obtain a
saturated updraft at the temperature implied by
is increased by
the latent heat of vaporization. In order to obtain to obtain a
saturated updraft at the temperature implied by 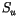 , we define
, we define
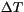 as the temperature perturbation in the updraft, then:
as the temperature perturbation in the updraft, then:
Substituting (4.22) and (4.23) into (4.21),
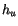 |
 |
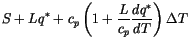 |
(4.24) |
| |
 |
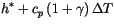 |
(4.25) |
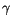 |
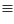 |
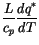 |
(4.26) |
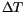 |
 |
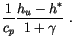 |
(4.27) |
The required updraft quantities are then
With 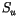 given by (4.28), (4.16) can be solved for
given by (4.28), (4.16) can be solved for
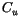 , then (4.19) and (4.20) can be solved for
, then (4.19) and (4.20) can be solved for 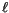 and
and 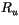 .
.
The expressions above require both the saturation specific humidity to
be
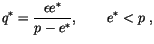 |
(4.30) |
where 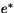 is the saturation vapor pressure, and its
dependence on temperature (in order to maintain saturation as the
temperature varies) to be
is the saturation vapor pressure, and its
dependence on temperature (in order to maintain saturation as the
temperature varies) to be
The deep convection scheme does not use the same approximation for the
saturation vapor pressure 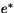 as is used in the rest of the
model. Instead,
as is used in the rest of the
model. Instead,
![$\displaystyle e^* = c_1 \exp\left[\frac{c_2(T - T_f)}{(T-T_f+c_3)} \right] ,$](img1237.gif) |
(4.34) |
where 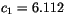 ,
, 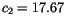 ,
, 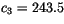 K and
K and
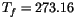 K is
the freezing point. For this approximation,
K is
the freezing point. For this approximation,
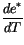 |
 |
![$\displaystyle e^* \frac{d}{dT} \left[\frac{c_2(T -
T_f)}{(T-T_f+c_3)} \right]$](img1243.gif) |
(4.35) |
| |
 |
![$\displaystyle e^*
\left[\frac{c_2}{(T-T_f+c_3)}
- \frac{c_2(T - T_f)}{(T-T_f+c_3)^2} \right]$](img1244.gif) |
(4.36) |
| |
 |
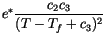 |
(4.37) |
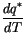 |
 |
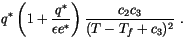 |
(4.38) |
We note that the expression for 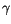 in the code gives
in the code gives
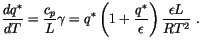 |
(4.39) |
The expressions for
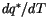 in (4.38) and
(4.39) are not identical. Also,
in (4.38) and
(4.39) are not identical. Also,
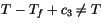 and
and
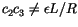 .
.
Downdrafts are assumed to exist whenever there is precipitation
production in the updraft ensemble where the downdrafts start at or
below the bottom of the updraft detrainment layer. Detrainment from
the downdrafts is confined to the sub-cloud layer, where all
downdrafts have the same mass flux at the top of the downdraft region.
Accordingly, the ensemble downdraft mass flux takes a similar form to
(4.13) but includes a ``proportionality factor'' to ensure that
the downdraft strength is physically consistent with precipitation
availability. This coefficient takes the form
![$\displaystyle \alpha = \mu \left [ \frac{P}{P + E_d} \right ] ,$](img1252.gif) |
(4.40) |
where 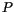 is the total precipitation in the convective layer and
is the total precipitation in the convective layer and 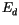 is the rain water evaporation required to maintain the downdraft in a
saturated state. This formalism ensures that the downdraft mass flux
vanishes in the absence of precipitation, and that evaporation cannot
exceed some fraction,
is the rain water evaporation required to maintain the downdraft in a
saturated state. This formalism ensures that the downdraft mass flux
vanishes in the absence of precipitation, and that evaporation cannot
exceed some fraction, 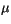 , of the precipitation, where
, of the precipitation, where 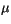 = 0.2.
= 0.2.
The parameterization is closed, i.e., the cloud base mass fluxes are
determined, as a function of the rate at which the cumulus consume
convective available potential energy (CAPE). Since the large-scale
temperature and moisture changes in both the cloud and sub-cloud layer
are linearly proportional to the cloud base updraft mass flux (e.g. see
eq. 4.2 - 4.5), the CAPE change due to convective
activity can be written as
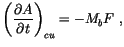 |
(4.41) |
where 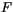 is the CAPE consumption rate per unit cloud base mass flux.
The closure condition is that the CAPE is consumed at an exponential
rate by cumulus convection with characteristic adjustment time scale
is the CAPE consumption rate per unit cloud base mass flux.
The closure condition is that the CAPE is consumed at an exponential
rate by cumulus convection with characteristic adjustment time scale
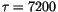 s:
s:
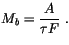 |
(4.42) |
The quantities 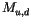 ,
, 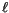 ,
, 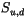 ,
, 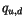 ,
, 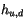 are
defined on layer interfaces, while
are
defined on layer interfaces, while 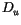 ,
, 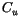 ,
, 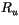 are defined on
layer midpoints.
are defined on
layer midpoints. 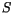 ,
, 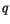 ,
, 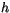 ,
, 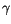 are required on both
midpoints and interfaces and the interface values
are required on both
midpoints and interfaces and the interface values
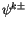 are
determined from the midpoint values
are
determined from the midpoint values 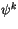 as
as
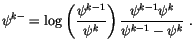 |
(4.43) |
All of the differencing within the deep convection is in height
coordinates. The differences are naturally taken as
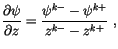 |
(4.44) |
where 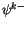 and
and 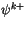 represent values on the upper and
lower interfaces, respectively for layer
represent values on the upper and
lower interfaces, respectively for layer  . The convention elsewhere
in this note (and elsewhere in the code) is
. The convention elsewhere
in this note (and elsewhere in the code) is
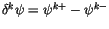 . Therefore, we avoid using the compact
. Therefore, we avoid using the compact 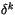 notation, except for height, and define
notation, except for height, and define
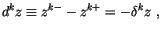 |
(4.45) |
so that 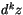 corresponds to the variable dz(k) in the deep
convection code.
corresponds to the variable dz(k) in the deep
convection code.
Although differences are in height coordinates, the equations are cast
in flux form and the tendencies are computed in units
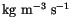 . The expected units are recovered at the end by multiplying by
. The expected units are recovered at the end by multiplying by
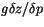 .
.
The environmental profiles at midpoints are
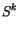 |
 |
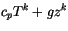 |
(4.46) |
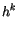 |
 |
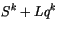 |
(4.47) |
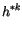 |
 |
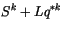 |
(4.48) |
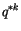 |
 |
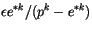 |
(4.49) |
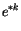 |
 |
![$\displaystyle c_1 \exp\left[\frac{c_2(T^k - T_f)}{(T^k-T_f+c_3)} \right]$](img1284.gif) |
(4.50) |
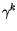 |
 |
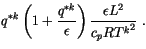 |
(4.51) |
The environmental profiles at interfaces of 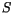 ,
, 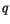 ,
, 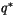 , and
, and
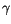 are determined using (4.43) if
are determined using (4.43) if
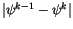 is large enough. However, there are
inconsistencies in what happens if
is large enough. However, there are
inconsistencies in what happens if
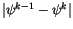 is not
large enough. For
is not
large enough. For 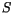 and
and 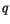 the condition is
the condition is
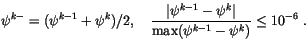 |
(4.52) |
For 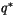 and
and 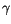 the condition is
the condition is
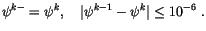 |
(4.53) |
Interface values of 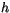 are not needed and interface values of
are not needed and interface values of 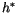 are given by
are given by
The unitless updraft mass flux (scaled by the inverse of the cloud base mass
flux) is given by differencing (4.13) as
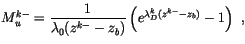 |
(4.55) |
with the boundary condition that
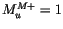 . The entrainment and
detrainment are calculated using
. The entrainment and
detrainment are calculated using
Note that 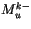 and
and 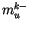 differ only by the value of
differ only by the value of
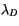 .
.
The updraft moist static energy is determined by differencing
(4.18)
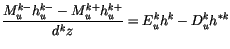 |
(4.59) |
![$\displaystyle h_u^{k-} = \frac{1}{M_u^{k-}}\left[M_u^{k+} h_u^{k+} + d^kz\left( E_u^k h^k - D_u^k h^{*k} \right)\right] ,$](img1303.gif) |
(4.60) |
with
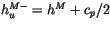 , where
, where 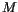 is the layer of maximum
is the layer of maximum 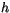 .
.
Once 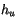 is determined, the lifting condensation level is found by
differencing (4.16) and (4.17) similarly to
(4.18):
is determined, the lifting condensation level is found by
differencing (4.16) and (4.17) similarly to
(4.18):
The detrainment of 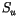 is given by
is given by 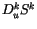 not by
not by
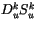 ,
since detrainment occurs at the environmental value of
,
since detrainment occurs at the environmental value of 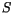 . The
detrainment of
. The
detrainment of 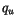 is given by
is given by
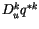 , even though the
updraft is not yet saturated. The LCL will usually occur below
, even though the
updraft is not yet saturated. The LCL will usually occur below 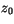 ,
the level at which detrainment begins, but this is not guaranteed.
,
the level at which detrainment begins, but this is not guaranteed.
The lower boundary conditions,
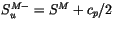 and
and
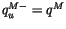 , are determined from the first midpoint values in the plume,
rather than from the interface values of
, are determined from the first midpoint values in the plume,
rather than from the interface values of 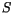 and
and 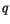 . The solution of
(4.61) and (4.62) continues upward until the
updraft is saturated according to the condition
. The solution of
(4.61) and (4.62) continues upward until the
updraft is saturated according to the condition
The condensation (in units of m ) is determined by a centered differencing of
(4.16):
) is determined by a centered differencing of
(4.16):
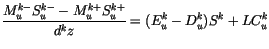 |
(4.65) |
The rain production (in units of m ) and condensed liquid are then determined by
differencing (4.19) as
) and condensed liquid are then determined by
differencing (4.19) as
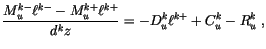 |
(4.67) |
and (4.20) as
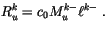 |
(4.68) |
Then
The CAM 3.0 provides the ability to transport constituents via
convection. The method used for constituent transport by deep
convection is a modification of the formulation described in
Zhang and McFarlane [199].
We assume the updrafts and downdrafts are described by a steady state
mass continuity equation for a ``bulk'' updraft or downdraft
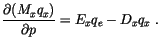 |
(4.72) |
The subscript 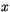 is used to denote the updraft (
is used to denote the updraft (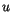 ) or downdraft
(
) or downdraft
(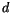 ) quantity.
) quantity. 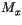 here is the mass flux in units of Pa/s defined at the
layer interfaces,
here is the mass flux in units of Pa/s defined at the
layer interfaces, 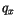 is the mixing ratio of the updraft or
downdraft.
is the mixing ratio of the updraft or
downdraft. 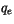 is the mixing ratio of the quantity in the
environment (that part of the grid volume not occupied by the up and
downdrafts).
is the mixing ratio of the quantity in the
environment (that part of the grid volume not occupied by the up and
downdrafts). 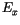 and
and 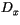 are the entrainment and detrainment rates
(units of s
are the entrainment and detrainment rates
(units of s ) for the up- and down-drafts. Updrafts are allowed
to entrain or detrain in any layer. Downdrafts are assumed to entrain
only, and all of the mass is assumed to be deposited into the surface
layer.
) for the up- and down-drafts. Updrafts are allowed
to entrain or detrain in any layer. Downdrafts are assumed to entrain
only, and all of the mass is assumed to be deposited into the surface
layer.
Equation 4.72 is first solved for up and downdraft mixing
ratios 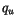 and
and 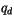 , assuming the environmental mixing ratio
, assuming the environmental mixing ratio 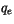 is the same as the gridbox averaged mixing ratio
is the same as the gridbox averaged mixing ratio 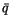 .
.
Given the up- and down-draft mixing ratios, the mass continuity
equation used to solve for the gridbox averaged mixing ratio 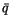 is
is
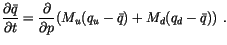 |
(4.73) |
These equations are solved for in subroutine CONVTRAN. There
are a few numerical details employed in CONVTRAN that are worth
mentioning here as well.
- mixing quantities needed at interfaces are calculated using the
geometric mean of the layer mean values.
- simple first order upstream biased finite differences are used
to solve 4.72 and 4.73.
- fluxes calculated at the interfaces are constrained so that the
resulting mixing ratios are positive definite. This means that
this parameterization is not suitable for moving mixing ratios of
quantities meant to represent perturbations of a trace constituent
about a mean value (in which case the quantity can meaningfully take
on positive and negative mixing ratios). The algorithm can be modified
in a straightforward fashion to remove this constraint, and provide
meaningful transport of perturbation quantities if necessary. the
reader is warned however that there are other places in the model code
where similar modifications are required because the model assumes
that all mixing ratios should be positive definite quantities.




Next: 4.2 Shallow/Middle Tropospheric Moist
Up: 4. Model Physics
Previous: 4. Model Physics
Contents
Jim McCaa
2004-06-22
![]() . The moist static energy in each plume
. The moist static energy in each plume ![]() is given by
is given by
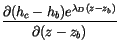
![]() is assumed
to be no lower than the mid-tropospheric minimum in saturated moist
static energy,
is assumed
to be no lower than the mid-tropospheric minimum in saturated moist
static energy, ![]() , ensuring that the cloud top detrainment is
confined to the conditionally stable portion of the atmospheric
column. All condensation is assumed to occur within the updraft
plumes, so that
, ensuring that the cloud top detrainment is
confined to the conditionally stable portion of the atmospheric
column. All condensation is assumed to occur within the updraft
plumes, so that ![]() . Each plume is assumed to have the same
value for the cloud base mass flux
. Each plume is assumed to have the same
value for the cloud base mass flux ![]() , which is specified
below. The vertical distribution of the cloud updraft mass flux is
given by
, which is specified
below. The vertical distribution of the cloud updraft mass flux is
given by
![]() , are:
, are:
![]() ,
, ![]() and
and ![]() are given by (4.13-4.15),
and
are given by (4.13-4.15),
and ![]() and
and ![]() are environmental profiles, (4.18) can be
solved for
are environmental profiles, (4.18) can be
solved for ![]() , given a lower boundary condition. The lower boundary
condition is obtained by adding a
, given a lower boundary condition. The lower boundary
condition is obtained by adding a ![]() K temperature perturbation to
the dry (and moist) static energy at cloud base, or
K temperature perturbation to
the dry (and moist) static energy at cloud base, or
![]() at
at ![]() . Below the lifting condensation level (LCL),
. Below the lifting condensation level (LCL),
![]() and
and ![]() are given by (4.16) and (4.17). Above
the LCL,
are given by (4.16) and (4.17). Above
the LCL, ![]() is reduced by condensation and
is reduced by condensation and ![]() is increased by
the latent heat of vaporization. In order to obtain to obtain a
saturated updraft at the temperature implied by
is increased by
the latent heat of vaporization. In order to obtain to obtain a
saturated updraft at the temperature implied by ![]() , we define
, we define
![]() as the temperature perturbation in the updraft, then:
as the temperature perturbation in the updraft, then:
![]() as is used in the rest of the
model. Instead,
as is used in the rest of the
model. Instead,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are
defined on layer interfaces, while
are
defined on layer interfaces, while ![]() ,
, ![]() ,
, ![]() are defined on
layer midpoints.
are defined on
layer midpoints. ![]() ,
, ![]() ,
, ![]() ,
, ![]() are required on both
midpoints and interfaces and the interface values
are required on both
midpoints and interfaces and the interface values
![]() are
determined from the midpoint values
are
determined from the midpoint values ![]() as
as
![]() . The expected units are recovered at the end by multiplying by
. The expected units are recovered at the end by multiplying by
![]() .
.
![]() is determined, the lifting condensation level is found by
differencing (4.16) and (4.17) similarly to
(4.18):
is determined, the lifting condensation level is found by
differencing (4.16) and (4.17) similarly to
(4.18):
![]() and
and
![]() , are determined from the first midpoint values in the plume,
rather than from the interface values of
, are determined from the first midpoint values in the plume,
rather than from the interface values of ![]() and
and ![]() . The solution of
(4.61) and (4.62) continues upward until the
updraft is saturated according to the condition
. The solution of
(4.61) and (4.62) continues upward until the
updraft is saturated according to the condition
![]() ) is determined by a centered differencing of
(4.16):
) is determined by a centered differencing of
(4.16):
![]() and
and ![]() , assuming the environmental mixing ratio
, assuming the environmental mixing ratio ![]() is the same as the gridbox averaged mixing ratio
is the same as the gridbox averaged mixing ratio ![]() .
.
![]() is
is