



Next: 4.3 Evaporation of convective
Up: 4. Model Physics
Previous: 4.1 Deep Convection
Contents
To characterize the convective forcing associated with shallow and
middle-level convection (i.e., convective activity not treated by the
primary convective parameterization scheme) we write the large-scale
budget equations for dry static energy and total water as
where
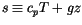 is the dry static energy;
is the dry static energy;  represents liquid water;
represents liquid water;
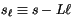 is the static
energy analogue of the liquid water potential temperature introduced
by Betts [18];
is the static
energy analogue of the liquid water potential temperature introduced
by Betts [18];  is the ``convective-scale'' liquid
water sink (sometimes denoted by
is the ``convective-scale'' liquid
water sink (sometimes denoted by 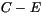 ); and
); and 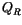 is the net
radiative heating rate. The subscript
is the net
radiative heating rate. The subscript 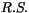 denotes the
resolvable-scale contributions to the large-scale budget. Note that
variations of the mean liquid water on the large scale have been
neglected. The barred quantities represent horizontal averages over
an area large enough to contain a collection of cloud elements, but
small enough so as to cover only a fraction of a large-scale
disturbance. By writing the mean thermodynamic variables in terms of
their average cloud and environment properties, and assuming that the
convection occupies only a small fraction of the averaging area, the
vertical eddy transports
denotes the
resolvable-scale contributions to the large-scale budget. Note that
variations of the mean liquid water on the large scale have been
neglected. The barred quantities represent horizontal averages over
an area large enough to contain a collection of cloud elements, but
small enough so as to cover only a fraction of a large-scale
disturbance. By writing the mean thermodynamic variables in terms of
their average cloud and environment properties, and assuming that the
convection occupies only a small fraction of the averaging area, the
vertical eddy transports
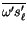 and
and
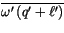 can
be approximated by the difference between the upward flux inside a
typical convective element and the downward flux (i.e. induced
subsidence) in the environment (cf. Yanai et al. [193]). Mathematically,
this approximation takes the form
can
be approximated by the difference between the upward flux inside a
typical convective element and the downward flux (i.e. induced
subsidence) in the environment (cf. Yanai et al. [193]). Mathematically,
this approximation takes the form
where 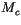 is a convective mass flux, and
is a convective mass flux, and 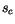 ,
, 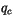 , and
, and 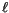 represent cloud-scale properties. Thus, (4.74) and
(4.75) can be written as
represent cloud-scale properties. Thus, (4.74) and
(4.75) can be written as
Let us now turn our attention to a vertically discrete model
atmosphere and consider the case where layers  and
and 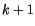 are moist
adiabatically unstable, i.e. a non-entraining parcel of air at level
are moist
adiabatically unstable, i.e. a non-entraining parcel of air at level
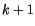 (with moist static energy
(with moist static energy 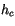 ) would be unstable if
raised to level
) would be unstable if
raised to level  . We assume the existence of a non-entraining
convective element with roots in level
. We assume the existence of a non-entraining
convective element with roots in level 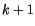 , condensation and rainout
processes in level
, condensation and rainout
processes in level  , and limited detrainment in level
, and limited detrainment in level 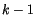 (see
Figure 4.1). In accordance with (4.78) and
(4.79), the discrete dry static energy and specific humidity
budget equations for these three layers can be written as
(see
Figure 4.1). In accordance with (4.78) and
(4.79), the discrete dry static energy and specific humidity
budget equations for these three layers can be written as
where the subscript 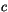 denotes cloud properties in the ascent region,
denotes cloud properties in the ascent region,
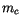 is a convective mass flux at the bottom of the condensation
layer (level
is a convective mass flux at the bottom of the condensation
layer (level
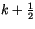 , ``cloud base''), and
, ``cloud base''), and 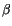 is a yet
to be determined ``detrainment parameter'' at level
is a yet
to be determined ``detrainment parameter'' at level
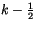 that will take a value between zero and one. Note that the
convective-scale liquid water sink
that will take a value between zero and one. Note that the
convective-scale liquid water sink 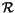 has been redefined in
terms of mass per unit area per unit time (denoted by
has been redefined in
terms of mass per unit area per unit time (denoted by 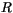 ), and the
resolvable-scale components have been dropped for the convenience of
the following discussion. In the general case, the thermodynamic
properties of the updraft region can be assumed to be equal to their
large-scale values in the sub-cloud layer, level
), and the
resolvable-scale components have been dropped for the convenience of
the following discussion. In the general case, the thermodynamic
properties of the updraft region can be assumed to be equal to their
large-scale values in the sub-cloud layer, level 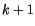 , plus some
arbitrary thermodynamic perturbation; i.e.
, plus some
arbitrary thermodynamic perturbation; i.e.
In the CAM 3.0 implementation of this scheme, when a sub-cloud layer
lies within the diagnosed atmospheric boundary layer, the perturbation
quantities
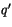 and
and 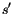 are assumed to be equal to
are assumed to be equal to
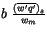 (e.g. see 4.470
and the atmospheric boundary layer discussion) and zero.
(e.g. see 4.470
and the atmospheric boundary layer discussion) and zero.
The liquid water generation rate at level  is given by
is given by
![$\displaystyle m_{c} \ell_k = m_{c} \left[ q_{c} - (q_c)_{_k} \right] .$](img1385.gif) |
(4.89) |
Using the saturation relation
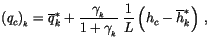 |
(4.90) |
where
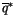 denotes the saturated specific humidity
denotes the saturated specific humidity
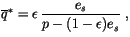 |
(4.91) |
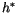 denotes the saturated moist state energy,
denotes the saturated moist state energy, 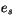 is the
saturation vapor pressure (determined from a precomputed table), and
is the
saturation vapor pressure (determined from a precomputed table), and
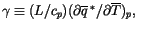 and assuming that the large-scale liquid water
divergence in layer
and assuming that the large-scale liquid water
divergence in layer  is zero, (4.89) can be manipulated to
give the rainout term in layer
is zero, (4.89) can be manipulated to
give the rainout term in layer  as
as
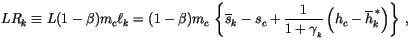 |
(4.92) |
and the liquid water flux into layer 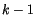 as
as
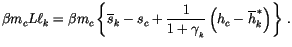 |
(4.93) |
Figure 4.1:
Conceptual three-level non-entraining cloud
model
|
|
Equations (4.82) and (4.85) can be combined to give an
equation for moist static energy in layer 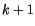
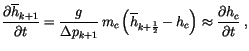 |
(4.94) |
where the approximation follows from the assumption that
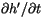 can be neglected. Using the relation
can be neglected. Using the relation
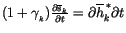 , (4.81) can be manipulated
to give an expression for the time rate of change of saturated moist
static energy in layer
, (4.81) can be manipulated
to give an expression for the time rate of change of saturated moist
static energy in layer 
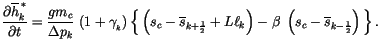 |
(4.95) |
Subtracting (4.95) from (4.94) results in
from which the convective mass flux 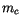 can be written as
can be written as
![$\displaystyle m_{c} = \frac{h_c - \overline{h}^{ *}_k} {g\tau \left\{ \frac{(...
...{1}{\Delta p_{k+1}} \left[\overline{h}_{k+\frac{1}{2}}- h_{c} \right] \right\}}$](img1402.gif) |
(4.97) |
where 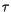 is a characteristic convective adjustment time scale.
is a characteristic convective adjustment time scale.
Physically realistic solutions require that the convective mass flux
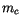 be positive, implying the following constraint on the
detrainment parameter
be positive, implying the following constraint on the
detrainment parameter 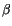
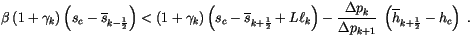 |
(4.98) |
A second physical constraint is imposed to ensure that the adjustment
process does not supersaturate the ``detrainment layer'', 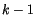 , which
leads to the following constraint on the detrainment parameter,
, which
leads to the following constraint on the detrainment parameter,
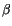 :
:
A final constraint on the adjustment process attempts to minimize the
introduction of
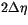 computational structures in the
thermodynamic field by not allowing the procedure to increase the
vertical gradient of
computational structures in the
thermodynamic field by not allowing the procedure to increase the
vertical gradient of 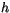 when
when
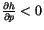 in
the upper pair of layers. Mathematically this constraint is
formulated by discretizing in time the moist static energy equations
in layers
in
the upper pair of layers. Mathematically this constraint is
formulated by discretizing in time the moist static energy equations
in layers  and
and 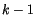 , leading to the following constraint on
, leading to the following constraint on
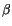
where 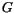 is an arbitrary vertical difference in the adjusted moist
static energy profile (cf. Hack et al. [66]).
is an arbitrary vertical difference in the adjusted moist
static energy profile (cf. Hack et al. [66]).
The first guess for the detrainment parameter, 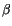 , comes from a
crude buoyancy argument where
, comes from a
crude buoyancy argument where
![$\displaystyle \beta = {\rm max} \begin{cases}\beta_{\rm min} \ [1ex] {\rm min}...
...a p_{k-1}} {(h_{c} - \overline{h}^{ *}_k) \Delta p_k} \end{cases} \end{cases}$](img1414.gif) |
(4.101) |
and
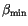 is assumed to be 0.10 (i.e., 10% detrainment).
Since
is assumed to be 0.10 (i.e., 10% detrainment).
Since 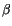 effectively determines the actual autoconversion from
cloud water to rainwater,
effectively determines the actual autoconversion from
cloud water to rainwater,
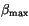 is determined from a
minimum autoconversion requirement which is mathematically written as
is determined from a
minimum autoconversion requirement which is mathematically written as
![$\displaystyle \beta_{\rm max} = {\rm max} \begin{cases}\beta_{\rm min} \ [1ex] 1 - c_0 ( \delta z - \delta z_{\rm min}) \end{cases}$](img1417.gif) |
(4.102) |
where 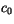 is a constant autoconversion coefficient assumed to be
equal to 1.0
is a constant autoconversion coefficient assumed to be
equal to 1.0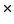 10
10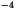 m
m ,
, 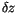 is the depth of
contiguous convective activity (i.e. layers in which condensation and
rainout takes place) including and below layer
is the depth of
contiguous convective activity (i.e. layers in which condensation and
rainout takes place) including and below layer  , and
, and
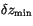 is a minimum depth for precipitating convection. The physical
constraints on the adjustment process are then applied to determine
the actual value of
is a minimum depth for precipitating convection. The physical
constraints on the adjustment process are then applied to determine
the actual value of 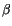 appropriate to the stabilization of
levels
appropriate to the stabilization of
levels  and
and 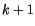 .
.
In summary, the adjustment procedure is applied as follows. A first
guess at 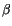 is determined from (4.101) and
(4.102), and further refined using (4.98),
(4.99), and (4.100). The convective mass flux,
is determined from (4.101) and
(4.102), and further refined using (4.98),
(4.99), and (4.100). The convective mass flux, 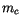 ,
is then determined from (4.97), followed by application of
budget equations (4.80)-(4.85) to complete the
thermodynamic adjustment in layers
,
is then determined from (4.97), followed by application of
budget equations (4.80)-(4.85) to complete the
thermodynamic adjustment in layers 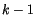 through
through 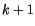 . By repeated
application of this procedure from the bottom of the model to the top,
the thermodynamic structure is locally stabilized, and a vertical
profile of the total cloud mass flux associated with shallow and
mid-level convection,
. By repeated
application of this procedure from the bottom of the model to the top,
the thermodynamic structure is locally stabilized, and a vertical
profile of the total cloud mass flux associated with shallow and
mid-level convection, 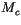 (where
(where
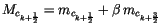 )
can be constructed. This mass flux profile can also be used to
estimate the convective-scale transport of arbitrary passive scalars.
The production rate of convective precipitation
)
can be constructed. This mass flux profile can also be used to
estimate the convective-scale transport of arbitrary passive scalars.
The production rate of convective precipitation 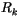 is supplied to
the parameterization of evaporation of convective precipitation
described in section 4.3. The free parameters for the
convection scheme consist of a minimum convective detrainment,
is supplied to
the parameterization of evaporation of convective precipitation
described in section 4.3. The free parameters for the
convection scheme consist of a minimum convective detrainment,
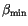 , a characteristic adjustment time scale for the
convection,
, a characteristic adjustment time scale for the
convection, 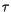 , a cloud-water to rain-water autoconversion
coefficient
, a cloud-water to rain-water autoconversion
coefficient 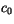 , and a minimum depth for precipitating convection
, and a minimum depth for precipitating convection
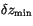 .
.




Next: 4.3 Evaporation of convective
Up: 4. Model Physics
Previous: 4.1 Deep Convection
Contents
Jim McCaa
2004-06-22
![]() and
and ![]() are moist
adiabatically unstable, i.e. a non-entraining parcel of air at level
are moist
adiabatically unstable, i.e. a non-entraining parcel of air at level
![]() (with moist static energy
(with moist static energy ![]() ) would be unstable if
raised to level
) would be unstable if
raised to level ![]() . We assume the existence of a non-entraining
convective element with roots in level
. We assume the existence of a non-entraining
convective element with roots in level ![]() , condensation and rainout
processes in level
, condensation and rainout
processes in level ![]() , and limited detrainment in level
, and limited detrainment in level ![]() (see
Figure 4.1). In accordance with (4.78) and
(4.79), the discrete dry static energy and specific humidity
budget equations for these three layers can be written as
(see
Figure 4.1). In accordance with (4.78) and
(4.79), the discrete dry static energy and specific humidity
budget equations for these three layers can be written as
![]() is given by
is given by
![]() be positive, implying the following constraint on the
detrainment parameter
be positive, implying the following constraint on the
detrainment parameter ![]()
![]() , comes from a
crude buoyancy argument where
, comes from a
crude buoyancy argument where
![]() is determined from (4.101) and
(4.102), and further refined using (4.98),
(4.99), and (4.100). The convective mass flux,
is determined from (4.101) and
(4.102), and further refined using (4.98),
(4.99), and (4.100). The convective mass flux, ![]() ,
is then determined from (4.97), followed by application of
budget equations (4.80)-(4.85) to complete the
thermodynamic adjustment in layers
,
is then determined from (4.97), followed by application of
budget equations (4.80)-(4.85) to complete the
thermodynamic adjustment in layers ![]() through
through ![]() . By repeated
application of this procedure from the bottom of the model to the top,
the thermodynamic structure is locally stabilized, and a vertical
profile of the total cloud mass flux associated with shallow and
mid-level convection,
. By repeated
application of this procedure from the bottom of the model to the top,
the thermodynamic structure is locally stabilized, and a vertical
profile of the total cloud mass flux associated with shallow and
mid-level convection, ![]() (where
(where
![]() )
can be constructed. This mass flux profile can also be used to
estimate the convective-scale transport of arbitrary passive scalars.
The production rate of convective precipitation
)
can be constructed. This mass flux profile can also be used to
estimate the convective-scale transport of arbitrary passive scalars.
The production rate of convective precipitation ![]() is supplied to
the parameterization of evaporation of convective precipitation
described in section 4.3. The free parameters for the
convection scheme consist of a minimum convective detrainment,
is supplied to
the parameterization of evaporation of convective precipitation
described in section 4.3. The free parameters for the
convection scheme consist of a minimum convective detrainment,
![]() , a characteristic adjustment time scale for the
convection,
, a characteristic adjustment time scale for the
convection, ![]() , a cloud-water to rain-water autoconversion
coefficient
, a cloud-water to rain-water autoconversion
coefficient ![]() , and a minimum depth for precipitating convection
, and a minimum depth for precipitating convection
![]() .
.