



Next: 7. Initial and Boundary
Up: 6. Sea Ice Thermodynamics
Previous: 6.8 Snow-Ice Conversion
Contents
Subsections
The heat content change within the sea ice over the time interval 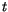 to
to 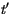 corresponding to temperatures
corresponding to temperatures 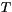 and
and 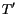 , respectively,
allowing for temperature dependent heat capacity, thermal conduction
(see section 6.6)
and internal absorption of penetrating solar radiation, is given by:
, respectively,
allowing for temperature dependent heat capacity, thermal conduction
(see section 6.6)
and internal absorption of penetrating solar radiation, is given by:
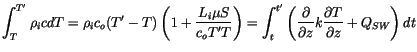 |
(6.52) |
The heat equation is discretized using a
backwards-Euler, space-centered scheme. Using a staggered grid with
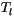 representing the layer temperature and
representing the layer temperature and 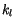 representing
conductivity at the layer interfaces, for interior layers we have
representing
conductivity at the layer interfaces, for interior layers we have
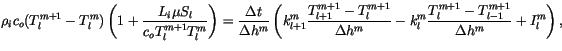 |
(6.53) |
where
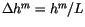 , the conductivity is
, the conductivity is
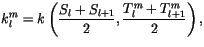 |
(6.54) |
and the absorbed solar radiation is
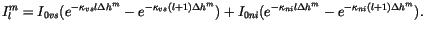 |
(6.55) |
Figure 6.1:
Vertical grid of the sea ice (a) when
snow is present and (b) when the ice is snow free;  is the thickness of an ice layer and
is the thickness of an ice layer and 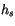 is the thickness of
the snow layer. The surface temperature in either case is
is the thickness of
the snow layer. The surface temperature in either case is
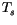 . Modified from Bitz and Lipscomb [20].
. Modified from Bitz and Lipscomb [20].
|
|
See Figure 6.1 for a diagram on the vertical level structure.
For a purely implicit backward scheme,  should be evaluated at the
should be evaluated at the
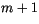 time level. However, when
time level. However, when  is evaluated at time level
is evaluated at time level 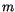 ,
experiments show that the solution is stable and converges to the same
solution one gets when evaluating
,
experiments show that the solution is stable and converges to the same
solution one gets when evaluating  at
at 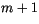 .
.
The discrete heat equation for the surface layers is modified slightly
from Eq. 6.53 to maintain second-order accuracy for
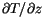 . The equation for the bottom layer (
. The equation for the bottom layer (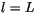 ) is
) is
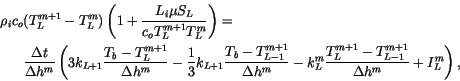 |
(6.56) |
where the 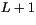 interface in contact with the underlying ocean is assumed
to be at temperature
interface in contact with the underlying ocean is assumed
to be at temperature
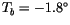 C, and where the conductivity is simply
C, and where the conductivity is simply
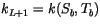 .
The equations for the top surface depend on the surface conditions,
of which there are four possibilities, as outlined in Table 6.2.
.
The equations for the top surface depend on the surface conditions,
of which there are four possibilities, as outlined in Table 6.2.
Table 6.2:
Top Surface Boundary Cases
| |
snow accumulated |
melting |
| case I |
yes |
no |
| case II |
no |
no |
| case III |
yes |
yes |
| case IV |
no |
yes |
The discrete heat equation for the
uppermost layer (i.e, the snow layer) is
![$\displaystyle \rho_s c_s(T_0^{m+1} - T_0^m) = { \Delta t \over h_s^m } \left[ k...
...^{m+1} \over h_s^m } - \beta k_s { T_1^{m+1} - T_s^{m+1} \over h_s^m } \right].$](img3087.gif) |
(6.57) |
The heat equation solver is formulated for the general case where the heat
capacity of snow 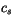 may be specified, although it is taken to be 0.
The parameters
may be specified, although it is taken to be 0.
The parameters 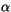 and
and 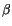 are defined to give second-order accurate
spatial differencing for
are defined to give second-order accurate
spatial differencing for
 across the
changing layer spacing at the snow/ice boundary;
across the
changing layer spacing at the snow/ice boundary;
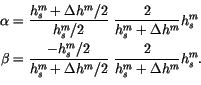 |
(6.58) |
The conductivity at the snow-ice interface is found by equating
conductive fluxes above and below the interface;
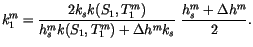 |
(6.59) |
Because 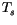 is below melting, a flux boundary condition is used, and an additional
equation is required in the coupled set:
is below melting, a flux boundary condition is used, and an additional
equation is required in the coupled set:
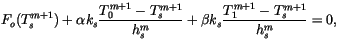 |
(6.60) |
where
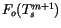 is the sum of all terms on the right-hand side
of Eq. 6.2 except
is the sum of all terms on the right-hand side
of Eq. 6.2 except
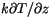 . The net surface
flux
. The net surface
flux
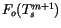 is approximated as linear in
is approximated as linear in 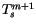 ; thus
; thus
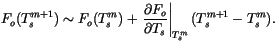 |
(6.61) |
with
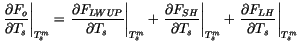 |
(6.62) |
To simplify our set of equations, we define
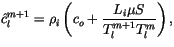 |
(6.63) |
where the hat implies that
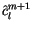 depends on
depends on 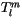 as well as on
as well as on 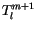 ,
and
,
and
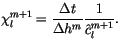 |
(6.64) |
Also, let
and suppress the index 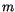 for
for 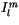 , so that
for interior layers (
, so that
for interior layers (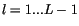 ),
),
where
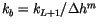 .
The equation describing the snow layer is written
.
The equation describing the snow layer is written
![$\displaystyle \rho_s c_s (T_0^{m+1}-T_0^m)={\Delta t \over h_s^m } \left[ k_1(T...
...m+1}) -\alpha k_0(T_0^{m+1}-T_s^{m+1}) -\beta k_0(T_1^{m+1}-T_s^{m+1}) \right].$](img3116.gif) |
(6.70) |
Finally, the flux boundary condition becomes
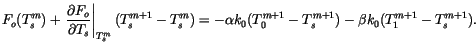 |
(6.71) |
The complete set of coupled equations for case I can be written with
all of the terms that explicitly depend on temperature at the 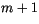 time step gathered on the right-hand side:
time step gathered on the right-hand side:
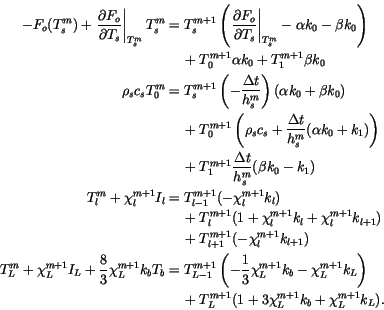 |
(6.72) |
These equations are subsequently related to
the following abbreviated form
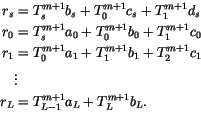 |
(6.73) |
The first two rows can be combined to eliminate the coefficient on
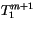 in the first row, allowing the set to be written in
tridiagonal form:
in the first row, allowing the set to be written in
tridiagonal form:
![\begin{displaymath}\begin{array}{l l l} r = \left[ \begin{array}{c} r_s c_0 - r_...
...m+1} \ T_1^{m+1} \ \vdots \ \end{array} \right]. \end{array}\end{displaymath}](img3121.gif) |
(6.74) |
Because the matrix A depends on
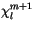 , which in turn depends
on
, which in turn depends
on 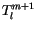 , the system of equations is solved iteratively. An initial
guess is used for the temperature dependence of
, the system of equations is solved iteratively. An initial
guess is used for the temperature dependence of
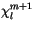 ,
and then
,
and then
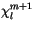 is updated successively after each iteration.
Under most conditions the method approaches a solution in less than
four iterations with a maximum error tolerance of
is updated successively after each iteration.
Under most conditions the method approaches a solution in less than
four iterations with a maximum error tolerance of
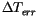 for
for
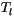 with an initial guess of
with an initial guess of
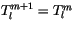 .
.
Nearly the same method applies when the ice is snow free, except one
less equation is needed to describe the evolution of the temperature
profile. The equation for the uppermost ice layer is written
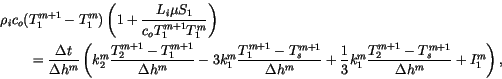 |
(6.75) |
where
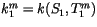 . After the definitions from Eqs.
6.63-6.65 are applied, Eq. 6.75 becomes
. After the definitions from Eqs.
6.63-6.65 are applied, Eq. 6.75 becomes
![$\displaystyle T_1^{m+1}-T_1^m=\chi_1^{m+1}\left[k_2(T_2^{m+1}-T_1^{m+1}) -3k_1(T_1^{m+1}-T_s^{m+1}) +{1 \over 3}k_1(T_2^{m+1}-T_s^{m+1})+I_1^m\right].$](img3127.gif) |
(6.76) |
The flux boundary condition follows
after linearizing
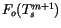 in
in 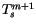 :
:
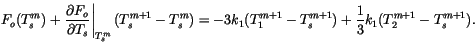 |
(6.77) |
The complete set of coupled equation includes Eqs. 6.72 for
layers 2 to L with the following two equations for the surface and
upper ice layer:
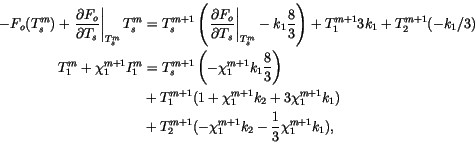 |
(6.78) |
which can be written
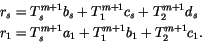 |
(6.79) |
These two equations can be combined to eliminate the coefficient on
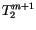 , allowing the set to be written in tridiagonal form:
, allowing the set to be written in tridiagonal form:
![\begin{displaymath}\begin{array}{l l l} r = \left[ \begin{array}{c} r_s c_1 - r_...
...m+1} \ T_2^{m+1} \ \vdots \ \end{array} \right]. \end{array}\end{displaymath}](img3132.gif) |
(6.80) |
As for case I, this system of equations must be solved iteratively.
Case III describes melting conditions in the presence of a snow layer
at the surface. Here a temperature boundary condition is used, which
simplifies the solution because the first row in Eqs. 6.72 is
not needed and
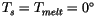 C in the second row. Hence the
complete set of coupled equations is identical to Eqs. 6.72 for
layers 1 to L, with the addition of an equation for the snow layer,
C in the second row. Hence the
complete set of coupled equations is identical to Eqs. 6.72 for
layers 1 to L, with the addition of an equation for the snow layer,
![$\displaystyle \rho_s c_s T_0^m + T_{melt} {\Delta t \over h_s } (\alpha + \beta...
... } (k_1+\alpha k_0 ) \right] - T_1^{m+1} {\Delta t \over h_s } (k_1-\beta k_0).$](img3134.gif) |
(6.81) |
This set of equations can be written in tridiagonal form, without the
need to eliminate any terms, as was required in cases I and II.
However, the solution must still be iterated.
Like case III, case IV describes melting conditions, but here the sea
ice is snow free. Hence, the first two rows of Eqs. 6.72
are not needed, and
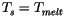 for
for 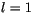 . The
set of coupled equations comprises those from Eqs. 6.72 for
layers 2 to L and the following equation for layer 1:
. The
set of coupled equations comprises those from Eqs. 6.72 for
layers 2 to L and the following equation for layer 1:
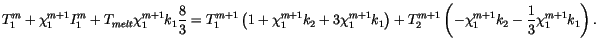 |
(6.82) |
As in case III, this set of equations can immediately be written in the
tridiagonal form and solved iteratively.
Figure 6.2:
Diagram showing energy content before (a) and after (b)
changing the layer spacing for an ice model with four vertical
layers that experiences melt at the top surface and growth at
the bottom surface. From [19]
|
|
The energy of melting of the ice and snow layers needs to be adjusted
when the layer spacing changes after growth/melt,
evaporation/sublimation, and flooding (see Figure 6.2).
This calculation is only made when CAM 3.0 is coupled to a mixed layer
ocean. The adjusted energy of melting is
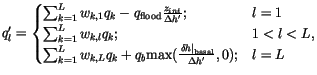 |
(6.83) |
where 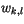 are weights computed from the relative overlap of
layer
are weights computed from the relative overlap of
layer 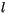 with each layer
with each layer  from the old layer spacing and
from the old layer spacing and 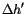 is the new layer spacing.
is the new layer spacing.




Next: 7. Initial and Boundary
Up: 6. Sea Ice Thermodynamics
Previous: 6.8 Snow-Ice Conversion
Contents
Jim McCaa
2004-06-22
![]() to
to ![]() corresponding to temperatures
corresponding to temperatures ![]() and
and ![]() , respectively,
allowing for temperature dependent heat capacity, thermal conduction
(see section 6.6)
and internal absorption of penetrating solar radiation, is given by:
, respectively,
allowing for temperature dependent heat capacity, thermal conduction
(see section 6.6)
and internal absorption of penetrating solar radiation, is given by:
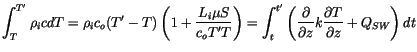
![]() representing the layer temperature and
representing the layer temperature and ![]() representing
conductivity at the layer interfaces, for interior layers we have
representing
conductivity at the layer interfaces, for interior layers we have
![\includegraphics[]{figures/figure6-1}](img3079.gif)
![]() should be evaluated at the
should be evaluated at the
![]() time level. However, when
time level. However, when ![]() is evaluated at time level
is evaluated at time level ![]() ,
experiments show that the solution is stable and converges to the same
solution one gets when evaluating
,
experiments show that the solution is stable and converges to the same
solution one gets when evaluating ![]() at
at ![]() .
.
![]() . The equation for the bottom layer (
. The equation for the bottom layer (![]() ) is
) is
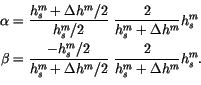
![]() time step gathered on the right-hand side:
time step gathered on the right-hand side:
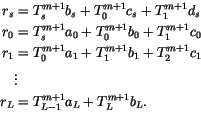
![\begin{displaymath}\begin{array}{l l l} r = \left[ \begin{array}{c} r_s c_0 - r_...
...m+1} \ T_1^{m+1} \ \vdots \ \end{array} \right]. \end{array}\end{displaymath}](img3121.gif)
![\begin{displaymath}\begin{array}{l l l} r = \left[ \begin{array}{c} r_s c_1 - r_...
...m+1} \ T_2^{m+1} \ \vdots \ \end{array} \right]. \end{array}\end{displaymath}](img3132.gif)
![]() C in the second row. Hence the
complete set of coupled equations is identical to Eqs. 6.72 for
layers 1 to L, with the addition of an equation for the snow layer,
C in the second row. Hence the
complete set of coupled equations is identical to Eqs. 6.72 for
layers 1 to L, with the addition of an equation for the snow layer,
![]() for
for ![]() . The
set of coupled equations comprises those from Eqs. 6.72 for
layers 2 to L and the following equation for layer 1:
. The
set of coupled equations comprises those from Eqs. 6.72 for
layers 2 to L and the following equation for layer 1:
![\includegraphics[]{figures/figure6-2}](img3138.gif)